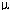 1(E
| T1 = t) 1(E
| T1 = t) |
= | 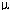 1(T1 = t | E) 1(T1 = t | E)
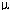 1(E) 1(E)
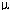 1(T1 =
t | E) 1(T1 =
t | E)
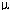 1(E)
+ 1(E)
+
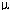 1(T1 =
t | F) 1(T1 =
t | F)
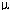 1(F) 1(F) |
| = | 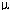 1(E) 1(E)----------- 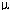 1(E)
+ 1(E)
+
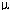 1(F) 1(F) |
|
| = |  -------  +
(1 +
(1  ) ) |
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
1. If this does not look immediately obvious, consider that either
E = [T2 = t] = my (Lizzi's) tth confirmation was lost,or
<em>F = [T2 = t] = my tth confirmation was received and Joanna's tth confirmation was lostmust occur, and that
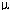 1(T1 = t
| E) =
1(T1 = t
| E) =
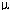 1(T1 = t
| F) = 1
because Lizzi can see her own computer screen, so we can apply Bayes'
Theorem as follows:
1(T1 = t
| F) = 1
because Lizzi can see her own computer screen, so we can apply Bayes'
Theorem as follows:
1(E | T1 = t)
= 1(T1 = t | E)
1(E)
1(T1 = t | E)
1(E) +
1(T1 = t | F)
1(F)
= 1(E)
-----------
1(E) +
1(F)
=
-------
+ (1
)
First published: August 27, 2001
Content last modified: August 27, 2001