Pick an arbitrary world

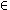
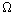 ,
and let
,
and let
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |

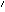
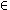
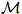 (
( )
iff
)
iff

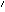 is reachable from
is reachable from
 .
.
Proof.
Pick an arbitrary world 
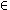
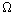 ,
and let
,
and let
(
) =
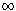
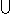
n = 1
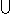
i 1, i 2, . . . , i nN
i n ( . . . (
i 2 (
i 1 (
) ) )
that is, 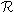 (
(  )
is the set of all worlds that are reachable from
)
is the set of all worlds that are reachable from  . Clearly, for each i
. Clearly, for each i 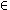 N,
N, 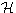 i(
i(  )
) 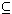
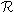 (
(  ),
which shows that
),
which shows that 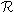 is a coarsening of the partitions
is a coarsening of the partitions 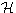 i, i
i, i 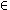 N.
Hence
N.
Hence 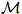 (
(  )
) 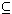
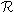 (
(  ),
as
),
as 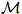 is the finest common coarsening of the
is the finest common coarsening of the 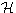 i's.
i's.
We need to show that 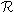 (
(  )
) 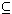
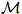 (
(  )
to complete the proof. To do this, it suffices to show that for any sequence i 1, i 2, . . . , i n
)
to complete the proof. To do this, it suffices to show that for any sequence i 1, i 2, . . . , i n 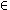 N
N
( 1 ) i n ( . . . (
i 2 (
i 1(
) ) )
We will prove ( 1 ) by induction on n. By definition, 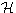 i(
i(  )
) 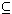
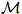 (
(  )
for each i
)
for each i 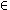 N, proving ( 1 ) for n = 1. Suppose now that ( 1 ) obtains for n = k, and for a given i
N, proving ( 1 ) for n = 1. Suppose now that ( 1 ) obtains for n = k, and for a given i 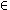 N, let
N, let  *
* 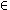
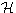 i( A )
where A =
i( A )
where A = 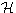 i k ( . . . (
i k ( . . . ( 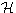 i 2 (
i 2 ( 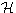 i 1 (
i 1 (  ) ) ).
By induction hypothesis, A
) ) ).
By induction hypothesis, A 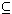
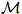 (
(  ).
Since
).
Since 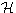 i( A )
states that i 1 thinks that i 2 thinks that . . . i k thinks that i thinks that
i( A )
states that i 1 thinks that i 2 thinks that . . . i k thinks that i thinks that  * is possible, A and
* is possible, A and 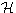 i(
i(  *)
must overlap, that is,
*)
must overlap, that is, 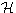 i(
i(  * )
* )  A
A 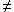
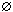 .
If
.
If  *
* 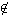
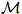 (
(  ),
then
),
then 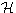 i(
i(  * )
* ) 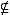
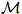 (
(  ),
which implies that
),
which implies that 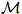 is not a common coarsening of the
is not a common coarsening of the  i's, a contradiction. Hence
i's, a contradiction. Hence  *
* 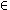
 (
(  ),
and since i was chosen arbitrarily from N, this shows that ( 1 ) obtains for n = k + 1.
),
and since i was chosen arbitrarily from N, this shows that ( 1 ) obtains for n = k + 1. 
| Peter Vanderschraaf peterv@cyrus.andrew.cmu.edu |