 3
3
bundle b
 2
2
bundle c
 1
1
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
version history
|
Stanford Encyclopedia of PhilosophyA | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
|
last substantive content change
|
Despite the fact that game theory has been rendered mathematically and logically systematic only recently, however, game-theoretic insights can be found among philosophers and political commentators going back to ancient times. For example, Plato, in the Republic, at one point has Socrates worry about the following situation. Consider a soldier at the front, waiting with his comrades to repulse an enemy attack. It may occur to him that if the defense is likely to be successful, then it isn't very probable that his own personal contribution will be essential. But if he stays, he runs the risk of being killed or wounded -- apparently for no point. On the other hand, if the enemy is going to win the battle, then his chances of death or injury are higher still, and now quite clearly to no point, since the line will be overwhelmed anyway. Based on this reasoning, it would appear that the soldier is better off running away regardless of who is going to win the battle. Of course, if all of the soldiers reason this way -- as they all apparently should, since they're all in identical situations -- then this will certainly bring about the outcome in which the battle is lost. Of course, this point, since it has occurred to us as analysts, can occur to the soldiers too. Does this give them a reason for staying at their posts? Just the contrary: the greater the soldiers' fear that the battle will be lost, the greater their incentive to get themselves out of harm's way. And the greater the soldiers' belief that the battle will be won, without the need of any particular individual's contributions, the less reason they have to stay and fight. If each soldier anticipates this sort of reasoning on the part of the others, all will quickly reason themselves into a panic, and their horrified commander will have a rout on his hands before the enemy has even fired a shot!
Long before game theory had come along to show people how to think about this sort of problem systematically, it had occurred to some actual military leaders and influenced their strategies. Thus the Spanish conqueror Cortez, when landing in Mexico with a small force who had good reason to fear their capacity to repel attack from the far more numerous Aztecs, removed the risk that his troops might think their way into a retreat by burning the ships on which they had landed. With retreat having thus been rendered physically impossible, the Spanish soldiers had no better course of action but to stand and fight -- and, furthermore, to fight with as much determination as they could muster. Better still, from Cortez's point of view, his action had a discouraging effect on the motivation of the Aztecs. He took care to burn his ships very visibly, so that the Aztecs would be sure to see what he had done. They then reasoned as follows: Any commander who could be so confident as to willfully destroy his own option to be prudent if the battle went badly for him must have good reasons for such extreme optimism. It cannot be wise to attack an opponent who has a good reason (whatever, exactly, it might be) for being sure that he can't lose. The Aztecs therefore retreated into the surrounding hills, and Cortez had his victory bloodlessly.
This situation, as imagined by Plato and as vividly acted upon by Cortez, has a deep and interesting logic. Notice that the soldiers are not motivated to retreat just, or even mainly, by their rational assessment of the dangers of battle and by their self-interest. Rather, they discover a sound reason to run away by realizing that what it makes sense for them to do depends on what it will make sense for others to do, and that all of the others can notice this too. Even a quite brave soldier may prefer to run rather than heroically, but pointlessly, die trying to stem the oncoming tide all by himself. Thus we could imagine, without contradiction, a circumstance in which an army, all of whose members are brave, flees at top speed before the enemy makes a move. If the soldiers really are brave, then this surely isn't the outcome any of them wanted; each would have preferred that all stand and fight. What we have here, then, is a case in which the interaction of many individually rational decision-making processes -- one process per soldier -- produces an outcome intended by no one. (Most armies try to avoid this problem just as Cortez did. Since they can't usually make retreat physically impossible, they make it economically impossible: they shoot deserters. Then standing and fighting is each soldier's individually rational course of action after all, because the cost of running is sure to be at least as high as the cost of staying.)
Another classic source that reproduces exactly this sequence of reasoning is Shakespeare. In Henry V, he has the victor of Agincourt explain his decision to slaughter French prisoners, in full view of the enemy, as follows. His own troops observe that the prisoners have been killed, and observe that the enemy has observed this. Therefore, they know what fate will await them at the enemy's hand if they don't win. Metaphorically, but very effectively, their boats have been burnt. The French prisoners died as a means by which Henry sent a signal to his own troops, thereby changing their incentives.
These examples might seem to be relevant only for those who find themselves in sordid situations of cut-throat competition. Perhaps, one might think, it is important for generals, politicians, businesspeople and others whose jobs involve manipulation of others, but the philosopher should only deplore its horrid morality. Such a conclusion would be highly premature, however. The study of the logic that governs the interrelationships amongst incentives, strategic interactions and outcomes has been fundamental in modern political philosophy, since centuries before anyone had an explicit name for this sort of logic.
Hobbes's Leviathan is often regarded as the founding work in modern political philosophy, the text that began the continuing round of analyses of the function and justification of the state and its restrictions on individual liberties. The core of Hobbes's reasoning can be given quite straightforwardly as follows. The best situation for all people is one in which each is free to do as she pleases. Often, such free people will wish to cooperate with one another in order to carry out projects that would be impossible for an individual acting alone. But if there are any immoral or amoral agents around, they will notice that their interests are best served by getting the benefits from cooperation and not returning them. Suppose, for example, that you agree to help me build my house in return for my promise to help you build yours. After my house is finished, I can make your labour free to me simply by reneging on my promise. I then realize, however, that if this leaves you with no house, you will have an incentive to take mine. This will put me in constant fear of you, and force me to spend valuable time and resources guarding myself against you. I can best minimize these costs by striking first and killing you at the first opportunity. Of course, you can anticipate all of this reasoning by me, and so have good reason to try to beat me to the punch. Since I can anticipate this reasoning by you, my original fear of you was not paranoid; nor was yours of me. In fact, neither of us actually needs to be immoral to get this chain of mutual reasoning going; we need only think that there is some possibility that the other might try to cheat on bargains. Once a small wedge of doubt enters any one mind, the incentive induced by fear of the consequences of being preempted -- hit before hitting first -- quickly becomes overwhelming on both sides. If either of us has any resources of our own that the other might want, this murderous logic will take hold long before we are so silly as to imagine that we could ever actually get so far as making deals to help one another build houses in the first place. Left to their own devices, rational agents will never derive the benefits of cooperation, and will instead live from the outset in a state of ‘war of all against all’, in Hobbes's words. In these circumstances, all human life, as he vividly and famously put it, will be "solitary, poor, nasty, brutish and short."
Hobbes's proposed solution to this problem was tyranny. The people can hire an agent -- a government -- whose job is to punish anyone who breaks any promise. So long as the threatened punishment is sufficiently dire -- Hobbes thought decapitation generally appropriate -- then the cost of reneging on promises will exceed the cost of keeping them. The logic here is identical to that used by an army when it threatens to shoot deserters. If all people know that these incentives hold for most others, then cooperation will not only be possible, but will be the expected norm, and the war of all against all becomes a general peace.
Hobbes pushes the logic of this argument to a very strong conclusion, arguing that it implies not only a government with the right and the power to enforce cooperation, but an ‘undivided’ government in which the arbitrary will of a single ruler must impose absolute obligation on all. Few contemporary political theorists think that the particular steps by which Hobbes reasons his way to this conclusion are both sound and valid. Working through these issues here, however, would carry us away from our topic into complex details of contractarian political philosophy. What is important in the present context is that these details, as they are in fact pursued in the contemporary debates, all involve sophisticated interpretation of the issues using the resources of modern game theory. Furthermore, Hobbes's most basic point, that the fundamental justification for the coercive authority and practices of governments is peoples' own need to protect themselves from what game theorists call ‘social dilemmas’, is accepted by many, if not most, political theorists. Notice that Hobbes has not argued that tyranny is a desirable thing in itself. The structure of his argument is that the logic of strategic interaction leaves only two general political outcomes possible: tyranny and anarchy. Rational agents then choose tyranny as the lesser of two evils.
The reasoning of Cortez, of Henry V and of Hobbes's political agents has a common logic, one derived from their situations. In each case, the aspect of the environment that is most important to the agents' achievement of their preferred outcomes is the set of expectations and possible reactions to their strategies by other agents. The distinction between acting parametrically on a passive world and acting non-parametrically on a world that tries to act in anticipation of these actions is fundamental. If you wish to kick a rock down a hill, you need only concern yourself with the rock's mass relative to the force of your blow, the extent to which it is bonded with its supporting surface, the slope of the ground on the other side of the rock, and the expected impact of the collision on your foot. The values of all of these variables are independent of your plans and intentions, since the rock has no interests of its own and takes no actions to attempt to assist or thwart you. By contrast, if you wish to kick a person down the hill, then unless that person is unconscious, bound or otherwise incapacitated, you will likely not succeed unless you can disguise your plans until it's too late for him to take either evasive or forestalling action. The logical issues associated with the second sort of situation are typically much more complicated, as a simple hypothetical example will illustrate.
Suppose first that you wish to cross a river that is spanned by three bridges. (Assume that swimming, wading or boating across are impossible.) The first bridge is known to be safe and free of obstacles; if you try to cross there, you will succeed. The second bridge lies beneath a cliff from which large rocks sometimes fall. The third is inhabited by deadly cobras. Now suppose you wish to rank-order the three bridges with respect to their preferability as crossing-points. Your task here is quite straightforward. The first bridge is obviously best, since it is safest. To rank-order the other two bridges, you require information about their relative levels of danger. If you can study the frequency of rock-falls and the movements of the cobras for awhile, you might be able to calculate that the cobra bridge is four times more dangerous than the rocky bridge, and the rocky bridge 20% more dangerous than the unobstructed bridge. Your reasoning here is strictly parametric because neither the rocks nor the cobras are trying to influence your actions, by, for example, concealing their typical patterns of behaviour because they know you are studying them. It is quite obvious what you should do here: cross at the safe bridge. Now let us complicate the situation a bit. Suppose that the bridge with the rocks was immediately before you, while the safe bridge was a day's difficult hike upstream. Your decision-making situation here is slightly more complicated, but it is still strictly parametric. You would have to decide whether the cost of the long hike was worth exchanging for the penalty of a 20% chance of being hit by a rock. However, this is all you must decide, and your probability of a successful crossing is entirely up to you; the environment is not interested in your plans.
However, if we now complicate the situation in the direction of non-parametricity, it becomes much more puzzling. Suppose that you are a fugitive of some sort, and waiting on the other side of the river with a gun is your pursuer. She will catch and shoot you, let us suppose, only if she waits at the bridge you try to cross; otherwise, you will escape. As you reason through your choice of bridge, it occurs to you that she is over there trying to anticipate your reasoning. It will seem that, surely, choosing the safe bridge straight away would be a mistake, since that is just where she will expect you, and your chances of death rise to certainty. So perhaps you should risk the rocks, since these odds are much better. But wait ... if you can reach this conclusion, your pursuer, who is just as rational and well-informed as you are, can anticipate that you will reach it, and will be waiting for you if you evade the rocks. So perhaps you must take your chances with the cobras; that is what she must least expect. But, then, no ... if she expects that you will expect that she will least expect this, then she will most expect it. This dilemma, you realize with dread, is general: you must do what your pursuer least expects; but whatever you most expect her to least expect is automatically what she will most expect. You appear to be trapped in indecision. All that might console you a bit here is that, on the other side of the river, your pursuer is trapped in exactly the same quandary, unable to decide which bridge to wait at because as soon as she imagines committing to one, she will notice that if she can find a best reason to pick a bridge, you can anticipate that same reason and then avoid her.
We know from experience that, in situations such as this, people do not usually stand and dither in circles forever. As we'll see later, there is a rational solution -- that is, a best rational action -- available to both players. However, until the 1940s neither philosophers nor economists knew how to find it mathematically. As a result, economists were forced to treat non-parametric influences as if they were complications on parametric ones. This is likely to strike the reader as odd, since, as our example of the bridge-crossing problem was meant to show, non-parametric features are often fundamental features of decision-making problems. Part of the explanation for game theory's relatively late entry into the field lies in the problems with which economists had historically been concerned. Classical economists, such as Adam Smith and David Ricardo, were mainly interested in the question of how agents in very large markets -- whole nations -- could interact so as to bring about maximum monetary wealth for themselves. Smith's basic insight, that efficiency is best maximized by agents freely seeking mutually advantageous bargains, was mathematically verified in the twentieth century. However, the demonstration of this fact applies only in conditions of ‘perfect competition,’ that is, when firms face no costs of entry or exit into markets, when there are no economies of scale, and when no agents' actions have unintended side-effects on other agents' well-being. Economists always recognized that this set of assumptions is purely an idealization for purposes of analysis, not a possible state of affairs anyone could try (or should want to try) to attain. But until the mathematics of game theory matured near the end of the 1970s, economists had to hope that the more closely a market approximates perfect competition, the more efficient it will be. No such hope, however, can be mathematically or logically justified in general; indeed, as a strict generalization the assumption can be shown to be false.
This article is not about the foundations of economics, but it is important for understanding the origins and scope of game theory to know that perfectly competitive markets have built into them a feature that renders them susceptible to parametric analysis. Because agents face no entry costs to markets, they will open shop in any given market until competition drives all profits to zero. This implies that if costs and demand are fixed, then agents have no options about how much to produce if they are trying to maximize the differences between their costs and their revenues. These production levels can be determined separately for each agent, so none need pay attention to what the others are doing; each agent treats her counterparts as passive features of the environment. The other kind of situation to which classical economic analysis can be applied without recourse to game theory is that of monopoly. Here, quite obviously, non-parametric considerations drop out, since there is only one agent under study. However, both perfect and monopolistic competition are very special and unusual market arrangements. Prior to the advent of game theory, therefore, economists were severely limited in the class of circumstances to which they could neatly apply their models.
Philosophers share with economists a professional interest in the conditions and techniques for the maximization of human welfare. In addition, philosophers have a special concern with the logical justification of actions, and often actions must be justified by reference to their expected outcomes. Without game theory, both of these problems resist analysis wherever non-parametric aspects are relevant. We will demonstrate this shortly by reference to the most famous (though not the most typical) game, the so-called Prisoner's Dilemma, and to other, more typical, games. In doing this, we will need to introduce, define and illustrate the basic elements and techniques of game theory. To this job we therefore now turn.
Though we might no longer be moved by scruples derived from psychological behaviorism, many theorists continue to follow Samuelson's way of understanding utility because they think it important that game theory apply to any kind of agent -- a person, a bear, a bee, a firm or a country -- and not just to agents with human minds. When such theorists say that agents act so as to maximize their utility, they want this to be part of the definition of what it is to be an agent, not an empirical claim about possible inner states and motivations. Samuelson's conception of utility, defined by way of Revealed Preference Theory (RPT) introduced in his classic paper (Samuelson (1938)) satisfies this demand.
Some other theorists understand the point of game theory differently. They view game theory as providing an explanatory account of strategic reasoning. For this idea to be applicable, we must suppose that agents at least sometimes do what they do in non-parametric settings because game-theoretic logic recommends certain actions as the rational ones. Still other theorists interpret game theory normatively, as advising agents on what to do in strategic contexts in order to maximize their utility. Fortunately for our purposes, all of these ways of thinking about the possible uses of game theory are compatible with the tautological interpretation of utility maximization. The philosophical differences are not idle from the perspective of the working game theorist, however. As we will see in a later section, those who hope to use game theory to explain strategic reasoning, as opposed to merely strategic behavior, face some special philosophical and practical problems.
Since game theory involves formal reasoning, we must have a device for thinking of utility maximization in mathematical terms. Such a device is called a utility function. The utility-map for an agent is called a ‘function’ because it maps ordered preferences onto the real numbers. Suppose that agent x prefers bundle a to bundle b and bundle b to bundle c. We then map these onto a list of numbers, where the function maps the highest-ranked bundle onto the largest number in the list, the second-highest-ranked bundle onto the next-largest number in the list, and so on, thus:
bundle aThe only property mapped by this function is order. The magnitudes of the numbers are irrelevant; that is, it must not be inferred that x gets 3 times as much utility from bundle a as she gets from bundle c. Thus we could represent exactly the same utility function as that above by3
bundle b
2
bundle c
1
bundle a7,326
bundle b
12.6
bundle c
−1,000,000
The numbers featuring in an ordinal utility function are thus not measuring any quantity of anything. A utility-function in which magnitudes do matter is called ‘cardinal’. Whenever someone refers to a utility function without specifying which kind is meant, you should assume that it's ordinal. These are the sorts we'll need for the first set of games we'll examine. Later, when we come to seeing how to solve games that involve randomization -- our river-crossing game from Part 1 above, for example -- we'll need to build cardinal utility functions. The technique for doing this was given by von Neumann & Morgenstern (1947), and was an essential aspect of their invention of game theory. For the moment, however, we will need only ordinal functions.
We assume that players are economically rational. That is, a player can (i) assess outcomes; (ii) calculate paths to outcomes; and (iii) choose actions that yield their most-preferred outcomes, given the actions of the other players. This rationality might in some cases be internally computed by the agent. In other cases, it might simply be embodied in behavioral dispositions built by natural, cultural or economic selection.
Each player in a game faces a choice among two or more possible strategies. A strategy is a predetermined ‘programme of play’ that tells her what actions to take in response to every possible strategy other players might use. The significance of the italicized phrase here will become clear when we take up some sample games below.
A crucial aspect of the specification of a game involves the information that players have when they choose strategies. The simplest games (from the perspective of logical structure) are those in which agents have perfect information, meaning that at every point where each agent's strategy tells her to take an action, she knows everything that has happened in the game up to that point. A board-game of sequential moves in which in which both players watch all the action (and know the rules in common), such as chess, is an instance of such a game. By contrast, the example of the bridge-crossing game from Section 1 above illustrates a game of imperfect information, since the fugitive must choose a bridge to cross without knowing the bridge at which the pursuer has chosen to wait, and the pursuer similarly makes her decision in ignorance of the actions of her quarry. Since game theory is about rational action given the strategically significant actions of others, it should not surprise you to be told that what agents in games know, or fail to know, about each others' actions makes a considerable difference to the logic of our analyses, as we will see.
It was said above that the distinction between sequential-move and simultaneous-move games is not identical to the distinction between perfect-information and imperfect-information games. Explaining why this is so is a good way of establishing full understanding of both sets of concepts. As simultaneous-move games were characterized in the previous paragraph, it must be true that all simultaneous-move games are games of imperfect information. However, some games may contain mixes of sequential and simultaneous moves. For example, two firms might commit to their marketing strategies independently and in secrecy from one another, but thereafter engage in pricing competition in full view of one another. If the optimal marketing strategies were partially or wholly dependent on what was expected to happen in the subsequent pricing game, then the two stages would need to be analyzed as a single game, in which a stage of sequential play followed a stage of simultaneous play. Whole games that involve mixed stages of this sort are games of imperfect information, however temporally staged they might be. Games of perfect information (as the name implies) denote cases where no moves are simultaneous (and where no player ever forgets what has gone before).
It was said above that games of perfect information are the (logically) simplest sorts of games. This is so because in such games (as long as the games are finite, that is, terminate after a known number of actions) players and analysts can use a straightforward procedure for predicting outcomes. A rational player in such a game chooses her first action by considering each series of responses and counter-responses that will result from each action open to her. She then asks herself which of the available final outcomes brings her the highest utility, and chooses the action that starts the chain leading to this outcome. This process is called backward induction (because the reasoning works backwards from eventual outcomes to present decision problems).
We will have much more to say about backward induction and its properties in a later section (when we come to discuss equilibrium and equilibrium selection). For now, we have described it just in order to use it to introduce one of the two types of mathematical objects used to represent games: game-trees. A game-tree is an example of what mathematicians call a directed graph. That is, it is a set of connected nodes in which the overall graph has a direction. We can draw trees from the top of the page to the bottom, or from left to right. In the first case, nodes at the top of the page are interpreted as coming earlier in the sequence of actions. In the case of a tree drawn from left to right, leftward nodes are prior in the sequence to rightward ones. An unlabelled tree has a structure of the following sort:
The point of representing games using trees can best be grasped by visualizing the use of them in supporting backward-induction reasoning. Just imagine the player (or analyst) beginning at the end of the tree, where outcomes are displayed, and then working backwards from these, looking for sets of strategies that describe paths leading to them. Since a player's utility function indicates which outcomes she prefers to which, we also know which paths she will prefer. Of course, not all paths will be possible because the other player has a role in selecting paths too, and won't take actions that lead to less preferred outcomes for him. We will present some examples of this interactive path-selection, and detailed techniques for reasoning through them, after we have described a situation we can use a tree to depict.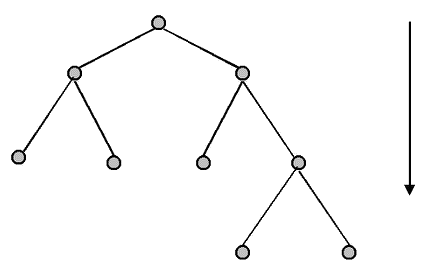
Figure 1
Trees are used to represent sequential games, because they show the order in which actions are taken by the players. However, games are sometimes represented on matrices rather than trees. This is the second type of mathematical object used to represent games. Matrices, unlike trees, simply show the outcomes, represented in terms of the players' utility functions, for every possible combination of strategies the players might use. For example, it makes sense to display the river-crossing game from Section 1 on a matrix, since in that game both the fugitive and the hunter have just one move each, and each chooses their move in ignorance of what the other has decided to do. Here, then, is part of the matrix:
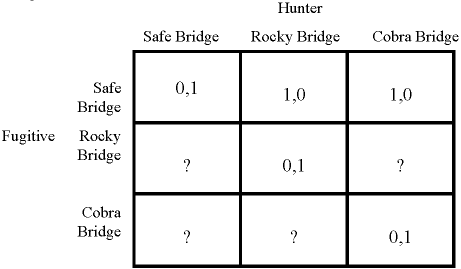
Figure 2
The fugitive's three possible strategies -- cross at the safe bridge, risk the rocks and risk the cobras -- form the rows of the matrix. Similarly, the hunter's three possible strategies -- waiting at the safe bridge, waiting at the rocky bridge and waiting at the cobra bridge -- form the columns of the matrix. Each cell of the matrix shows -- or, rather would show if our matrix was complete -- an outcome defined in terms of the players' payoffs. A player's payoff is simply the number assigned by her ordinal utility function to the state of affairs corresponding to the outcome in question. For each outcome, Row's payoff is always listed first, followed by Column's. Thus, for example, the upper left-hand corner above shows that when the fugitive crosses at the safe bridge and the hunter is waiting there, the fugitive gets a payoff of 0 and the hunter gets a payoff of 1. We interpret these by reference to their utility functions, which in this game are very simple. If the fugitive gets safely across the river he receives a payoff of 1; if he doesn't he gets 0. If the fugitive doesn't make it, either because he's shot by the hunter or hit by a rock or struck by a cobra, then the hunter gets a payoff of 1 and the fugitive gets a payoff of 0.
We'll briefly explain the parts of the matrix that have been filled in, and then say why we can't yet complete the rest. Whenever the hunter waits at the bridge chosen by the fugitive, the fugitive is shot. These outcomes all deliver the payoff vector (0, 1). You can find them descending diagonally across the matrix above from the upper right-hand corner. Whenever the fugitive chooses the safe bridge but the hunter waits at another, the fugitive gets safely across, yielding the payoff vector (1, 0). These two outcomes are shown in the second two cells of the top row. All of the other cells are marked, for now, with question marks. Why? The problem here is that if the fugitive crosses at either the rocky bridge or the cobra bridge, he introduces parametric factors into the game. In these cases, he takes on some risk of getting killed, and so producing the payoff vector (0, 1), that is independent of anything the hunter does. We don't yet have enough concepts introduced to be able to show how to represent these outcomes in terms of utility functions -- but by the time we're finished we will, and this will provide the key to solving our puzzle from Section 1.
Matrix games are referred to as ‘normal-form’ or ‘strategic-form’ games, and games as trees are referred to as ‘extensive-form’ games. The two sorts of games are not equivalent, because extensive-form games contain information -- about sequences of play and players' levels of information about the game structure -- that strategic-form games do not. In general, a strategic-form game could represent any one of several extensive-form games, so a strategic-form game is best thought of as being a set of extensive-form games. When order of play is irrelevant to a game's outcome, then you should study its strategic form, since it's the whole set you want to know about. Where order of play is relevant, the extensive form must be specified or your conclusions will be unreliable.
The name of the Prisoner's Dilemma game is derived from the following situation typically used to exemplify it. Suppose that the police have arrested two people whom they know have committed an armed robbery together. Unfortunately, they lack enough admissible evidence to get a jury to convict. They do, however, have enough evidence to send each prisoner away for two years for theft of the getaway car. The chief inspector now makes the following offer to each prisoner: If you will confess to the robbery, implicating your partner, and she does not also confess, then you'll go free and she'll get ten years. If you both confess, you'll each get 5 years. If neither of you confess, then you'll each get two years for the auto theft.
Our first step in modeling your situation as a game is to represent it in terms of utility functions. Both you and your partner's utility functions are identical:
Go freeThe numbers in the function above are now used to express your and your partner's payoffs in the various outcomes possible in your situation. We will refer to you as ‘Player I’ and to your partner as ‘Player II’. Now we can represent your entire situation on a matrix; this is the strategic form of your game:4
2 years
3
5 years
2
10 years
0
Each cell of the matrix gives the payoffs to both players for each combination of actions. Player I's payoff appears as the first number of each pair, Player II's as the second. So, if both of you confess you each get a payoff of 2 (5 years in prison each). This appears in the upper-left cell. If neither of you confess, you each get a payoff of 3 (2 years in prison each). This appears as the lower-right cell. If you confess and your partner doesn't you get a payoff of 4 (going free) and she gets a payoff of 0 (ten years in prison). This appears in the upper-right cell. The reverse situation, in which she confesses and you refuse, appears in the lower-left cell.
Figure 3
You evaluate your two possible actions here by comparing your payoffs in each column, since this shows you which of your actions is preferable for each possible action by your partner. So, observe: If your partner confesses than you get a payoff of 2 by confessing and a payoff of 0 by refusing. If your partner refuses, you get a payoff of 4 by confessing and a payoff of 3 by refusing. Therefore, you're better off confessing regardless of what she does. Your partner, meanwhile, evaluates her actions by comparing her payoffs down each row, and she comes to exactly the same conclusion that you do. Wherever one action for a player is superior to her other actions for each possible action by the opponent, we say that the first action strictly dominates the second one. In the PD, then, confessing strictly dominates refusing for both players. Both players know this about each other, thus entirely eliminating any temptation to depart from the strictly dominated path. Thus both players will confess, and both will go to prison for 5 years.
The players, and analysts, can predict this outcome using a mechanical procedure, known as iterated elimination of strictly dominated strategies. You, as Player 1, can see by examining the matrix that your payoffs in each cell of the top row are higher than your payoffs in each corresponding cell of the bottom row. Therefore, it can never be rational for you to play your bottom-row strategy, viz., refusing to confess, regardless of what your opponent does. Since your bottom-row strategy will never be played, we can simply delete the bottom row from the matrix. Now it is obvious that Player II will not refuse to confess, since his payoff from confessing in the two cells that remain is higher than his payoff from refusing. So, once again, we can delete the one-cell column on the left from the game. We now have only one cell remaining, that corresponding to the outcome brought about by mutual confession. Since the reasoning that led us to delete all other possible outcomes depended at each step only on the premise that both players are economically rational - that is, prefer higher payoffs to lower ones - there is very strong grounds for viewing joint confession as the solution to the game, the outcome on which its play must converge. You should note that the order in which strictly dominated rows and columns are deleted doesn't matter. Had we begun by deleting the right-hand column and then deleted the bottom row, we would have arrived at the same solution.
It's been said a couple of times that the PD is not a typical game in many respects. One of these respects is that all its rows and columns are either strictly dominated or strictly dominant. In any strategic-form game where this is true, iterated elimination of strictly dominated strategies is guaranteed to yield a unique solution. Later, however, we will see that for many games this condition does not apply, and then our analytic task is less straightforward.
You will probably have noticed something disturbing about the outcome of the PD. Had you both refused to confess, you'd have arrived at the lower-right outcome in which you each go to prison for only 2 years, thereby both earning higher utility than you receive when you confess. This is the most important fact about the PD, and its significance for game theory is quite general. We'll therefore return to it below when we discuss equilibrium concepts in game theory. For now, however, let us stay with our use of this particular game to illustrate the difference between strategic and extensive forms.
When people introduce the PD into popular discussions, you will sometimes hear them say that the police inspector must lock his prisoners into separate rooms so that they can't communicate with one another. The reasoning behind this idea seems obvious: if you could communicate, you'd surely see that you're both better off refusing, and could make an agreement to do so, no? This, one presumes, would remove your conviction that you must confess because you'll otherwise be sold up the river by your partner. In fact, however, this intuition is misleading and its conclusion is false.
When we represent the PD as a strategic-form game, we implicitly assume that the prisoners can't attempt collusive agreement since they choose their actions simultaneously. In this case, agreement before the fact can't help. If you are convinced that your partner will stick to the bargain then you can seize the opportunity to go scot-free by confessing. Of course, you realize that the same temptation will occur to her; but in that case you again want to make sure you confess, as this is your only means of avoiding your worst outcome. Your agreement comes to naught because you have no way of enforcing it; it constitutes what game theorists call ‘cheap talk’.
But now suppose that you do not move simultaneously. That is, suppose that one of you can choose after observing the other's action. This is the sort of situation that people who think non-communication important must have in mind. Now you can see that your partner has remained steadfast when it comes to your choice, and you need not be concerned about being suckered. However, this doesn't change anything, a point that is best made by re-representing the game in extensive form. This gives us our opportunity to introduce game-trees and the method of analysis appropriate to them.
First, however, here are definitions of some concepts that will be helpful in analyzing game-trees:
Node: A point at which a player takes an action.These quick definitions may not mean very much to you until you follow them being put to use in our analyses of trees below. It will probably be best if you scroll back and forth between them and the examples as we work through them. By the time you understand each example, you'll find the concepts and their definitions quite natural and intuitive.Initial node: The point at which the first action in the game occurs.
Terminal node: Any node which, if reached, ends the game. Each terminal node corresponds to an outcome.
Subgame: Any set of nodes and branches descending uniquely from one node.
Payoff: an ordinal utility number assigned to a player at an outcome.
Outcome: an assignment of a set of payoffs, one to each player in the game.
Strategy: a program instructing a player which action to take at every node in the tree where she could possibly be called on to make a choice.
To make this exercise maximally instructive, let's suppose that you and your partner have studied the matrix above and, seeing that you're both better off in the outcome represented by the lower-right cell, have formed an agreement to cooperate. You are to commit to refusal first, at which point she will reciprocate. We will refer to a strategy of keeping the agreement as ‘cooperation’, and will denote it in the tree below with ‘C’. We will refer to a strategy of breaking the agreement as ‘defection’, and will denote it on the tree below with ‘D’. As before, you are I and your partner is II. Each node is numbered 1, 2, 3, ... , from top to bottom, for ease of reference in discussion. Here, then, is the tree:
Look first at each of the terminal nodes (those along the bottom). These represent possible outcomes. Each is identified with a assignment of payoffs, just as in the strategic-form game, with I's payoff appearing first in each set and II's appearing second. Each of the structures descending from the nodes 1, 2 and 3 respectively is a sub-game. We begin our backward-induction analysis -- using a technique called Zermelo's algorithm -- with the sub-games that arise last in the sequence of play. If the subgame descending from node 3 is played, then Player II will face a choice between a payoff of 4 and a payoff of 3. (Consult the second number, representing her payoff, in each set at a terminal node descending from node 3.) II earns her higher payoff by playing D. We may therefore replace the entire subgame with an assignment of the payoff (0, 4) directly to node 3, since this is the outcome that will be realized if the game reaches that node. Now consider the subgame descending from node 2. Here, II faces a choice between a payoff of 2 and one of 0. She obtains her higher one, 2, by playing D. We may therefore assign the payoff (2,2) directly to node 2. Now we move to the subgame descending from node 1. (This subgame is, of course, identical to the whole game; all games are subgames of themselves.) You (Player I) now face a choice between outcomes (2,2) and (0,4). Consulting the first numbers in each of these sets, you see that you get your higher payoff -- 2 -- by playing D. D is, of course, the option of confessing. So you confess, and then your partner also confesses, yielding the same outcome as in the strategic-form representation.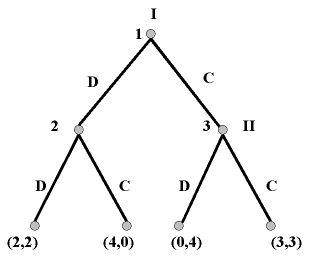
Figure 4
What has happened here is that you realize that if you play C (refuse to confess) at node 1, then your partner will be able to maximize her utility by suckering you and playing D. (On the tree, this happens at node 3.) This leaves you with a payoff of 0 (ten years in prison), which you can avoid only by playing D to begin with. You therefore defect from the agreement.
We have thus seen that in the case of the Prisoner's Dilemma, the simultaneous and sequential versions yield the same outcome. This will often not be true, however. In particular, only finite extensive-form (sequential) games of perfect information can be solved using Zermelo's algorithm.
As noted earlier in this section, sometimes we must represent simultaneous moves within games that are otherwise sequential. (As we said above, in all such cases the game as a whole will be one of imperfect information, so we won't be able to solve it using Zermelo's algorithm.) We represent such games using the device of information sets. Consider the following tree:
The oval drawn around nodes b and c indicates that they lie within a common information set. This means that at these nodes players cannot infer back up the path from whence they came; II does not know, in choosing her strategy, whether she is at b or c. (For this reason, what properly bear numbers in extensive-form games are information sets, conceived as ‘action points’, rather than nodes themselves; this is why the nodes inside the oval are labelled with letters rather than numbers.) Put another way, II, when choosing, does not know what I has done at node a. But you will recall from earlier in this section that this is just what defines two moves as simultaneous. We can thus see that the method of representing games as trees is entirely general. If no node after the initial node is alone in an information set on its tree, so that the game has only one subgame (itself), then the whole game is one of simultaneous play. If at least one node shares its information set with another, while others are alone, the game involves both simultaneous and sequential play, and so is still a game of imperfect information. Only if all information sets are inhabited by just one node do we have a game of perfect information.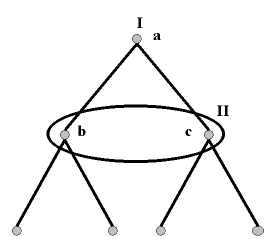
Figure 5
It's useful to start the discussion here from the case of the Prisoner's Dilemma because it's unusually simple from the perspective of these puzzles. What we referred to as its ‘solution’ is the unique Nash equilibrium of the game. (The ‘Nash’ here refers to John Nash, the Nobel Prize-winning mathematician who in Nash (1950) did most to extend and generalize von Neumann & Morgenstern's pioneering work.) Nash equilibrium (henceforth ‘NE’) applies (or fails to apply, as the case may be) to whole sets of strategies, one for each player in a game. A set of strategies is a NE just in case no player could improve her payoff, given the strategies of all other players in the game, by changing her strategy. Notice how closely this idea is related to the idea of strict dominance: no strategy could be a NE strategy if it is strictly dominated. Therefore, if iterative elimination of strictly dominated strategies takes us to a unique outcome, we know we have found the game's unique NE. Now, almost all theorists agree that avoidance of strictly dominated strategies is a minimum requirement of rationality. This implies that if a game has an outcome that is a unique NE, as in the case of joint confession in the PD, that must be its unique solution. This is one of the most important respects in which the PD is an ‘easy’ (and atypical) game.
We can specify one class of games in which NE is always not only necessary but sufficient as a solution concept. These are finite perfect-information games that are also zero-sum. A zero-sum game (in the case of a game involving just two players) is one in which one player can only be made better off by making the other player worse off. (Tic-tac-toe is a simple example of such a game: any move that brings me closer to winning brings you closer to losing, and vice-versa.) We can determine whether a game is zero-sum by examining players' utility functions: in zero-sum games these will be mirror-images of each other, with one player's highly ranked outcomes being low-ranked for the other and vice-versa. In such a game, if I am playing a strategy such that, given your strategy, I can't do any better, and if you are also playing such a strategy, then, since any change of strategy by me would have to make you worse off and vice-versa, it follows that our game can have no solution compatible with our mutual rationality other than its unique NE. We can put this another way: in a zero-sum game, my playing a strategy that maximizes my minimum payoff if you play the best you can, and your simultaneously doing the same thing, is just equivalent to our both playing our best strategies, so this pair of so-called ‘maximin’ procedures is guaranteed to find the unique solution to the game, which is its unique NE. (In tic-tac-toe, this is a draw. You can't do any better than drawing, and neither can I, if both of us are trying to win and trying not to lose.)
However, most games do not have this property. It won't be possible, in this one article, to enumerate all of the ways in which games can be problematic from the perspective of their possible solutions. (For one thing, it is highly unlikely that theorists have yet discovered all of the possible problems!) However, we can try to generalize the issues a bit.
First, there is the problem that in most non-zero-sum games, there is more than one NE, but not all NE look equally plausible as the solutions upon which strategically rational players would hit. Consider the strategic-form game below (taken from Kreps (1990), p. 403):
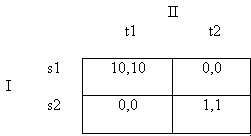
Figure 6
This game has two NE: s1-t1 and s2-t2. (Note that no rows or columns are strictly dominated here. But if Player I is playing s1 then Player II can do no better than t1, and vice-versa; and similarly for the s2-t2 pair.) If NE is our only solution concept, then we shall be forced to say that either of these outcomes is equally persuasive as a solution. However, if game theory is regarded as an explanatory and/or normative theory of strategic reasoning, this seems to be leaving something out: surely rational players with perfect information would converge on s1-t1? (Note that this is not like the situation in the PD, where the socially superior situation is unachievable because it is not a NE. In the case of the game above, both players have every reason to try to converge on the NE in which they are better off.)
This illustrates the fact that NE is a relatively (logically) weak solution concept, often failing to predict intuitively sensible solutions because, if applied alone, it refuses to allow players to use principles of equilibrium selection that, if not demanded by rationality, are at least not irrational. Consider another example from Kreps (1990), p. 397:
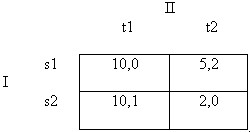
Figure 7
Here, no strategy strictly dominates another. However, Player I's top row, s1, weakly dominates s2, since I does at least as well using s1 as s2 for any reply by Player II, and on one reply by II (t2), I does better. So should not the players (and the analyst) delete the weakly dominated row s2? When they do so, column t1 is then strictly dominated, and the NE s1-t2 is selected as the unique solution. However, as Kreps goes on to show using this example, the idea that weakly dominated strategies should be deleted just like strict ones has odd consequences. Suppose we change the payoffs of the game just a bit, as follows:
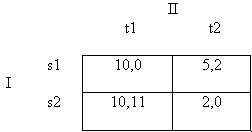
Figure 8
s2 is still weakly dominated as before; but of our two NE, s2-t1 is now the most attractive for both players; so why should the analyst eliminate its possibility? (Note that this game, again, does not replicate the logic of the PD. There, it makes sense to eliminate the most attractive outcome, joint refusal to confess, because both players have incentives to unilaterally deviate from it, so it is not an NE. This is not true of s2-t1 in the present game. You should be starting to clearly see why we called the PD game ‘atypical’.) The argument for eliminating weakly dominated strategies is that Player 1 may be nervous, fearing that Player II is not completely sure to be rational (or that Player II fears that Player I isn't completely rational, or that Player II fears that Player I fears that Player II isn't completely rational, and so on ad infinitum) and so might play t2 with some positive probability. If the possibility of departures from rationality is taken seriously, then we have an argument for eliminating weakly dominated strategies: Player I thereby insures herself against her worst outcome, s2-t2. Of course, she pays a cost for this insurance, reducing her expected payoff from 10 to 5. On the other hand, we might imagine that the players could communicate before playing the game and agree play correlated strategies so as to coordinate on s2-t1, thereby removing some, most or all of the uncertainty that encourages elimination of the weakly dominated row s1, and eliminating s1-t2 as a viable NE instead!
Any proposed principle for solving games that may have the effect of eliminating one or more NE from consideration is referred to as a refinement of NE. In the case just discussed, elimination of weakly dominated strategies is one possible refinement, since it refines away the NE s2-t1, and correlation is another, since it refines away the other NE, s1-t2, instead. So which refinement is more appropriate as a solution concept? People who think of game theory as an explanatory and/or normative theory of strategic rationality have generated a substantial literature in which the merits and drawbacks of a large number of refinements are debated. In principle, there seems to be no limit on the number of refinements that could be considered, since there may also be no limits on the set of philosophical intuitions about what principles a rational agent might or might not see fit to follow or to fear or hope that other players are following.
Behaviorists take a dim view of much of this activity. They see the job of game theory as being to predict outcomes given some distribution of strategic dispositions, and some distribution of expectations about the strategic dispositions of others, that have been shaped by institutional processes and / or evolutionary selection. (See Section 7 for further discussion.) On this view, which NE are viable in a game is determined by the underlying dynamics that equipped players with dispositions prior to the commencement of a game. The strategic natures of players are thereby treated as a set of exogenous inputs to the game, just as utility functions are. Behaviorists are thus less inclined to seek general refinements of the equilibrium concept itself, at least insofar as these involve the modeling of more sophisticated expressions of rationality over and above merely consistent maximization of utility. Behaviorists are often inclined to doubt that the goal of seeking a general theory of rationality makes sense as a project. Institutions and evolutionary processes build many environments, and what counts as rational procedure in one environment may not be favoured in another. Economic rationality requires only that agents have consistent preferences, that is, that they not prefer a to b and b to c and c to a. A great many arrangements of strategic dispositions are compatible with this minimal requirement, and evolutionary or institutional processes might generate games in any of them. On this view, NE is a robust equilibrium concept because if players evolve their strategic dispositions in settings that are competitive, those who don't do what's optimal given the strategies of others in that specific environment will be outcompeted, and so selection will either eliminate them or encourage the learning of new dispositions. There is no more ‘refined’ concept of rationality of which this can be argued to be true in general; and so, according to behaviorists, refinements of NE based on refinements of rationality are likely to be of merely occasional interest.
This does not imply that behaviorists abjure all ways of restricting sets of NE to plausible subsets. In particular, they tend to be sympathetic to approaches that shift emphasis from rationality itself onto considerations of the informational dynamics of games. We should perhaps not be surprised that NE analysis alone often fails to tell us much of interest about strategic-form games (e.g., Figure 6 above), in which informational structure is suppressed. Equilibrium selection issues are often more fruitfully addressed in the context of extensive-form games.
Consider the game described by this tree:
This game is not intended to fit any preconceived situation; it is simply a mathematical object in search of an application. (L and R here just denote ‘left’ and ‘right’ respectively.)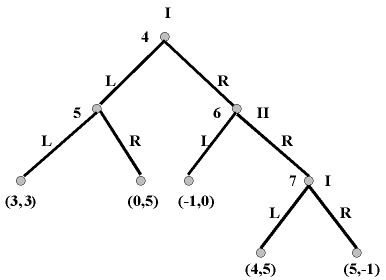
Figure 9
Now consider the strategic form of this game:
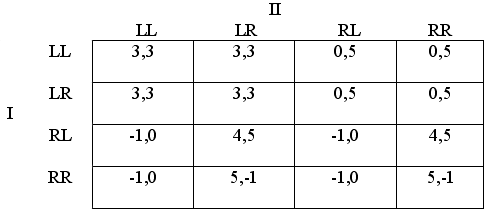
Figure 10
(If you are confused by this, remember that a strategy must tell a player what to do at every information set where that player has an action. Since each player chooses between two actions at each of two information sets here, each player has four strategies in total. The first letter in each strategy designation tells each player what to do if he or she reaches their first information set, the second what to do if their second information set is reached. I.e., LR for Player II tells II to play L if information set 5 is reached and R if information set 6 is reached.) If you examine this matrix, you will discover that (LL, RL) is among the NE. This is a bit puzzling, since if Player I reaches her second information set (7) in the extensive-form game, I would hardly wish to play L there; she earns a higher payoff by playing R at node 7. Mere NE analysis doesn't notice this because NE is insensitive to what happens off the path of play. Player I, in choosing L at node 4, ensures that node 7 will not be reached; this is what is meant by saying that it is ‘off the path of play’. In analyzing extensive-form games, however, we should care what happens off the path of play, because consideration of this is crucial to what happens on the path. For example, it is the fact that Player I would play R if node 7 were reached that would cause Player II to play L if node 6 were reached, and this is why Player I won't choose R at node 4. We are throwing away information relevant to game solutions if we ignore off-path outcomes, as mere NE analysis does. Notice that this reason for doubting that NE is a wholly satisfactory equilibrium concept in itself has nothing to do with intuitions about rationality, as in the case of the refinement concepts discussed in Section 2.5.
Now apply Zermelo's algorithm to the extensive form of our current example. Begin, again, with the last subgame, that descending from node 7. This is Player I's move, and she would choose R because she prefers her payoff of 5 to the payoff of 4 she gets by playing L. Therefore, we assign the payoff (5, -1) to node 7. Thus at node 6 II faces a choice between (-1, 0) and (5, -1). He chooses L. At node 5 II chooses R. At node 4 I is thus choosing between (0, 5) and (-1, 0), and so plays L. Note that, as in the PD, an outcome appears at a terminal node -- (4, 5) from node 7 -- that is Pareto superior to the NE. Again, however, the dynamics of the game prevent it from being reached.
The fact that Zermelo's algorithm picks out the strategy vector (LR, RL) as the unique solution to the game shows that it's yielding something other than just an NE. In fact, it is generating the game's subgame perfect equilibrium (SPE). It gives an outcome that yields a NE not just in the whole game but in every subgame as well. This is an extremely persuasive solution concept because, again unlike the refinements of Section 2.5, it does not demand ‘more’ rationality of agents, but less. The agents, at every node, simply choose the path that brings them the highest payoff in the subgame emanating from that node; and, then, in solving the game, they foresee that they will all do that. Agents who proceed in this way are said to be modular rational, that is, short-run rational at each step. They do not imagine themselves, by some fancy processes of hyper-rationality, acting against their local preferences for the sake of some wider goal. Note that, as in the PD, this can lead to outcomes which might be regretted from the social point of view. In our current example, Player I would be better off, and Player II no worse off, at the left-hand node emanating from node 7 than at the SPE outcome. But Player I's very modular rationality, and Player II's awareness of this, blocks the socially efficient outcome. If our players wish to bring about the more equitable outcome (4,5) here, they must do so by redesigning their institutions so as to change the structures of the games they play. Merely wishing that they could be hyper-rational in some way does not seem altogether coherent as an approach.
This way of thinking leads to serious misunderstandings of game theory, and so must be dispelled. Let us first introduce some terminology for talking about outcomes. Welfare economists typically measure social good in terms of Pareto efficiency. A distribution of utility β is said to be Pareto dominant over another distribution δ just in case from state δ there is a possible redistribution of utility to β such that at least one player is better off in β than in δ and no player is worse off. Failure to move to a Pareto-dominant redistribution is inefficient because the existence of β as a logical possibility shows that in δ some utility is being wasted. Now, the outcome (3,3) that represents mutual cooperation in our model of the PD is clearly Pareto dominant over mutual defection; at (3,3) both players are better off than at (2,2). So it is true that PDs lead to inefficient outcomes. This was true of our example in Section 2.6 as well.
However, inefficiency should not be associated with immorality. A utility function for a player is supposed to represent everything that player cares about, which may be anything at all. As we have described the situation of our prisoners they do indeed care only about their own relative prison sentences, but there is nothing essential in this. What makes a game an instance of the PD is strictly and only its payoff structure. Thus we could have two Mother Theresa types here, both of whom care little for themselves and wish only to feed starving children. But suppose the original Mother Theresa wishes to feed the children of Calcutta while Mother Juanita wishes to feed the children of Bogota. And suppose that the international aid agency will maximize its donation if the two saints nominate the same city, will give the second-highest amount if they nominate each others' cities, and the lowest amount if they each nominate their own city. Our saints are in a PD here, though hardly selfish or unconcerned with the social good.
To return to our prisoners, suppose that, contrary to our assumptions, they do value each other's well-being as well as their own. In that case, this must be reflected in their utility functions, and hence in their payoffs. If their payoff structures are changed, they will no longer be in a PD. But all this shows is that not every possible situation is a PD; it does not show that the threat of inefficient outcomes is a special artifact of selfishness. It is the logic of the prisoners' situation, not their psychology, that traps them in the inefficient outcome, and if that really is their situation then they are stuck in it (barring further complications to be discussed below). Agents who wish to avoid inefficient outcomes are best advised to prevent certain games from arising; the defender of the possibility of hyper-rationality is really proposing that they try to dig themselves out of such games by turning themselves into different kinds of agents.
In general, then, a game is partly defined by the payoffs assigned to the players. If a proposed solution involves tacitly changing these payoffs, then this ‘solution’ is in fact a disguised way of changing the subject.
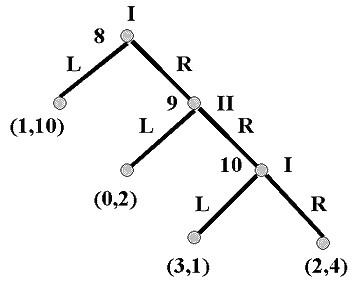
Figure 11
The NE outcome here is at the single leftmost node descending from node 8. To see this, backward induct again. At node 10, I would play L for a payoff of 3, giving II a payoff of 1. II can do better than this by playing L at node 9, giving I a payoff of 0. I can do better than this by playing L at node 8; so that is what I does, and the game terminates without II getting to move. But, now, notice the reasoning required to support this prediction. I plays L at node 8 because she knows that II is rational, and so would, at node 9, play L because II knows that I is rational and so would, at node 10, play L. But now we have the following paradox: I must suppose that II, at node 9, would predict I's rational play at node 10 despite having arrived at a node (9) that could only be reached if I is not rational! If I is not rational then II is not justified in predicting that I will not play R at node 10, in which case it is not clear that II shouldn't play R at 9; and if II plays R at 9, then I is guaranteed of a better payoff then she gets if she plays L at node 8. Both players must use backward induction to solve the game; backward induction requires that I know that II knows that I is rational; but II can solve the game only by using a backward induction argument that takes as a premise the irrationality of I. This is the paradox of backward induction.
A standard way around this paradox in the literature is to invoke the so-called ‘trembling hand’ due to Selten (1975). The idea here is that a decision and its consequent act may ‘come apart’ with some nonzero probability, however small. That is, a player might intend to take an action but then slip up in the execution and send the game down some other path instead. If there is even a remote possibility that a player may make a mistake -- that her ‘hand may tremble’ -- then no contradiction is introduced by a player's using a backward induction argument that requires the hypothetical assumption that another player has taken a path that a rational player could not choose. In our example, II could reason about what to do at node 9 conditional on the assumption that I rationally chose L at node 8 but then slipped.
There is a substantial technical literature on this backward-induction paradox, of which Bicchieri (1993) is the most comprehensive source. (Bicchieri, it should be noted, does not endorse an appeal to trembling hands as the appropriate solution. Discussing her particular proposal here would, however, take us too far afield into technicalities. The interested reader should study her book.) The puzzle has been introduced here just in order to point out that refinements of the type discussed in Section 2.6 can be encouraged by more than mere intuitions about the concept of rationality. For if hands may tremble than merely economically rational players will be motivated to worry about the probabilities with which apparent departures from rational play will be observed. For example, if my opponent's hand may tremble, then this gives me good reason to avoid the weakly dominated strategy s2 in the third example from Section 2.5. After all, my opponent might promise to play t1 in that game, and I may believe his promise; but if his hand then trembles and a play of t2 results, I get my worst payoff. If I'm risk-averse, then in such situations it would seem that I should stick to weakly dominant strategies.
The reader won't be surprised to hear that the behaviorist has a reply to this. He argues that when a player considers what would happen at nodes reachable only along out-of-equilibrium paths, he need merely refer to possible worlds in which the subgames beginning at the nodes in question exist by themselves (i.e., detached from the remainders of the games in which they occur). This might seem like an ad hoc resort; but it is not clear that it is any less so than is appeal to trembling hands, which find no independent motivation from elsewhere in economic theory or the theory of rational choice. In any case, appeal to possible worlds is a common strategy in science according to many philosophers. The issue is raised here not with any hope in mind of saying something conclusive about it, but just to give the reader some further sense of the philosophical issues that generate controversy in the foundations of game theory.
Suppose that we ignore rocks and cobras for a moment, and imagine that the bridges are equally safe. In this case, the fugitive's best course is to roll a three-sided die, in which each side represents a different bridge (or, more conventionally, a six-sided die in which each bridge is represented by two sides). He must then pre-commit himself to using whichever bridge is selected by this randomizing device. Against this strategy, the pursuer's best reply is to also use a three-sided die of her own. The fugitive now has a 2/3 probability of escaping and the pursuer a 1/3 probability of catching him. The fugitive cannot improve on these odds if the pursuer is randomizing, since to favour one bridge merely provides the pursuer with a pattern that can be exploited. Identical reasoning applies to the pursuer. Therefore, the two randomizing strategies are best replies to one another, and are therefore in Nash equilibrium.
Now let us re-introduce the parametric factors, that is, the falling rocks at bridge #2 and the cobras at bridge #3. Again, suppose that bridge #3 (cobras) is four times more dangerous for the fugitive than bridge #2 (rocks), while bridge #2 is 20% more dangerous than bridge #1 (unobstructed). We can solve this new game if we make certain assumptions about the two players' utility functions. Suppose that Player 1, the fugitive, cares only about living or dying (preferring life to death) while the pursuer simply wishes to be able to report that the fugitive is dead, preferring this to having to report that he got away. (In other words, neither player cares about how the fugitive lives or dies.) In this case, the fugitive simply takes his original randomizing formula and weights it according to the different levels of parametric danger at the three bridges. Each bridge should be thought of as a lottery over the fugitive's possible outcomes, in which each lottery has a different expected payoff in terms of the items in his utility function.
Consider matters from the pursuer's point of view. She will be using her NE strategy when she chooses the mix of probabilities over the three bridges that makes the fugitive indifferent amongst them as crossing points. The bridge with rocks is 1.2 times more dangerous for him than the safe bridge. Therefore, he will be indifferent between the two when the pursuer is 1.2 times more likely to be waiting at the safe bridge than the rocky bridge. The cobra bridge is 4 times more dangerous for the fugitive than the rocky bridge. Therefore, he will be indifferent between these two bridges when the pursuer's probability of waiting at the rocky bridge is 4 times higher than the probability that she is at the cobra bridge. This gives us an indifference ratio amongst the bridges of 4.8:4:1. Suppose that no mixed strategy involving use of the cobra bridge is dominated by a mixed strategy involving use of only the other two bridges (i.e., that the cobra bridge is not so dangerous that the hunter can't make the fugitive indifferent between its use and that of the other at any value). Since the probabilities must sum to 100, we find the probability with which the pursuer waits at each bridge by solving the following equation:
4.8x + 4x + x = 100x here equals 10.2. So at Nash equilibrium the pursuer must appear at the cobra bridge with a probability of .102, at the rocky bridge with a probability of .408, and the safe bridge with a probability of .489. These probabilities tell her how to weight her die before throwing it. The fugitive's NE strategy is, of course, as before: knowing that the pursuer will randomize so as to leave him indifferent, he will choose each bridge with equal probability.
We were able to solve this game straightforwardly because we set the utility functions in such a way as to make it zero-sum, or strictly competitive. That is, every gain in expected utility by one player represents a precisely symmetrical loss by the other. However, this condition may often not hold. Suppose now that the utility functions are more complicated. The pursuer most prefers an outcome in which she shoots the fugitive and so claims credit for his apprehension to one in which he dies of rockfall or snakebite; and she prefers this second outcome to his escape. The fugitive prefers a quick death by gunshot to the pain of being crushed or the terror of an encounter with a cobra. Most of all, of course, he prefers to escape. We cannot solve this game, as before, simply on the basis of knowing the players' ordinal utility functions, since the intensities of their respective preferences will now be relevant to their strategies.
Prior to the work of von Neumann & Morgenstern (1947), situations of this sort were inherently baffling to analysts. This is because utility does not denote a hidden psychological variable such as pleasure. As we discussed in Section 2.1, utility is merely a measure of relative behavioural dispositions given certain consistency assumptions about relations between preferences and choices. It therefore makes no sense to imagine comparing our players' cardinal -- that is, intensity-sensitive -- preferences with one another's, since there is no independent, interpersonally constant yardstick we could use. How, then, can we model games in which cardinal information is relevant? After all, modeling games requires that all players' utilities be taken simultaneously into account, as we've seen.
A crucial aspect of von Neumann & Morgenstern's (1947) work was the solution to this problem. Here, we will provide a brief outline of their ingenious technique for building cardinal utility functions out of ordinal ones. It is emphasized that what follows is merely an outline, so as to make cardinal utility non-mysterious to you as a student who is interested in knowing about the philosophical foundations of game theory, and about the range of problems to which it can be applied. Providing a manual you could follow in building your own cardinal utility functions would require many pages. Fortunately, such manuals are available in many textbooks. In any case, if you are a philosophy student you may not wish to attempt this until you've taken a course in probability theory.
Suppose we have an agent whose ordinal utility function is known. Indeed, suppose that it's our river-crossing fugitive. Let's assign him the following ordinal utility function:
EscapeNow, we know that his preference for escape over any form of death is likely to be stronger than his preference for, say, shooting over snakebite. This should be reflected in his choice behaviour in the following way. In a situation such as the river-crossing game, he should be willing to run greater risks to increase the relative probability of escape over shooting than he is to increase the relative probability of shooting over snakebite. This bit of logic is the crucial insight behind von Neumann & Morgenstern's (1947) solution to the cardinalization problem.4
Death by shooting
3
Death by rockfall
2
Death by snakebite
1
Begin by asking our agent to pick, from the available set of outcomes, a best one and a worst one. ‘Best’ and ‘worst’ are defined in terms of rational choice: a rational agent always chooses so as to maximize the probability of the best outcome -- call this W -- and to minimize the probability of the worst outcome -- call this L. Now consider prizes intermediate between W and L. We find, for a set of outcomes containing such prizes, a lottery over them such that our agent is indifferent between that lottery and a lottery including only W and L. In our example, this would be a lottery having shooting and rockfall as its possible outcomes. Call this lottery T . We define a utility function q = u(T) such that if q is the expected prize in T , the agent is indifferent between winning T and winning a lottery in which W occurs with probability u(T) and L occurs with probability 1 − u(T).
We now construct a compound lottery T* over the outcome set {W, L} such that the agent is indifferent between T and T*. A compound lottery is one in which the prize in the lottery is another lottery. This makes sense because, after all, it is still W and L that are at stake for our agent in both cases; so we can then analyze T* into a simple lottery over W and L. Call this lottery r. It follows from transitivity that T is equivalent to r. (Note that this presupposes that our agent does not gain utility from the complexity of her gambles.) The rational agent will now choose the action that maximizes the probability of winning W. The mapping from the set of outcomes to u(r) is a von Neumann-Morgenstern utility function (VNMuf).
What exactly have we done here? We've simply given our agent choices over lotteries, instead of over prizes directly, and observed how much extra risk he's willing to run to increase the chances of winning escape over snakebite relative to getting shot or clobbered with a rock. A VNMuf yields a cardinal, rather than an ordinal, measure of utility. Our choice of endpoint-values, W and L, is arbitrary, as before; but once these are fixed the values of the intermediate points are determined. Therefore, the VNMuf does measure the relative preference intensities of a single agent. However, since our assignment of utility values to W and L is arbitrary, we can't use VNMufs to compare the cardinal preferences of one agent with those of another. Furthermore, since we are using a risk-metric as our measuring instrument, the construction of the new utility function depends on assuming that our agent's attitude to risk itself stays constant from one comparison of lotteries to another. This seems reasonable for a single agent in a single game-situation. However, two agents in one game, or one agent under different sorts of circumstances, may display very different attitudes to risk. Perhaps in the river-crossing game the pursuer, whose life is not at stake, will enjoy gambling with her glory while our fugitive is cautious. In general, a risk-averse agent prefers a guaranteed prize to its equivalent expected value in a lottery. A risk-loving agent has the reverse preference. A risk-neutral agent is indifferent between these options. In analyzing the river-crossing game, however, we don't have to be able to compare the pursuer's cardinal utilities with the fugitive's. Both agents, after all, can find their NE strategies if they can estimate the probabilities each will assign to the actions of the other. This means that each must know both VNMufs; but neither need try to comparatively value the outcomes over which they're gambling.
We can now fill in the rest of the matrix for the bridge-crossing game that we started to draw in Section 2. If all that the fugitive cares about is life and death, but not the manner of death, and if all the hunter cares about is preventing the fugitive from escaping, then we can now interpret both utility functions cardinally. This permits us to assign expected utilities, expressed by multiplying the original payoffs by the relevant probabilities, as outcomes in the matrix. Suppose that the hunter waits at the cobra bridge with probability x and at the rocky bridge with probability y. Since her probabilities across the three bridges must sum to 1, this implies that she must wait at the safe bridge with probability 1 − (x + y). Then, continuing to assign the fugitive a payoff of 0 if he dies and 1 if he escapes, and the hunter the reverse payoffs, our complete matrix is as follows:
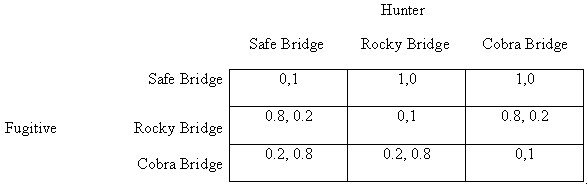
Figure 12
We can now read the following facts about the game directly from the matrix. No rows or columns strictly or weakly dominate any others. Therefore, the game's NE must be in mixed strategies.
Here is an odd feature of our analysis of the river-crossing game above. In the situation as we have imagined it, the fugitive knows that the hunter is least likely to cross at the cobra bridge. Yet we have told her to select a bridge at which to wait by flipping a coin. This process gives a non-zero probability of selecting the cobra bridge. Yet, surely, if the coin selects the cobra bridge it cannot be rational for the hunter to do as it directs. Won't she feel like a bit of an idiot standing there, knowing that the fugitive is probably waltzing across the safe bridge, or the relatively safe rocky bridge? Note that she will not feel torn in this situation if she plays this game with fugitives on a regular basis (and they know this). In that case, it is perfectly reasonable that she must sometimes wait at the cobra bridge, lest all fugitives be able to do better than their odds at NE by using the cobra bridge more often. Now, as far as the behaviorist is concerned this ends the matter. If the hunter and the fugitive have regularly played games that structurally resemble this river-crossing game, then selection pressures will have encouraged habits in them that lead them both to play its NE strategies and to sincerely rationalize doing so by means of some satisfying story or other. If neither party has ever been in a situation like this, and if their biological and/or cultural ancestors haven't either, and if neither is concerned with revealing information to opponents in expected future situations of this sort, then their behavior should be predicted not by a game theorist but by friends of theirs who are familiar with their personal idiosyncracies. Behaviorists are happy to recognize that game theory isn't useful for every decision problem, or even every strategic decision problem, that comes along.
However, the philosopher who wants game theory to serve as a descriptive and/or normative theory of strategic rationality cannot rest content with this answer. He must find a satisfying line of advice for the players even when their game is alone in the universe of strategic problems. No such advice can be given that is uncontroversially satisfactory -- behaviorists, after all, are often behaviorists because they aren't satisfied by any available approach here -= but there is a way of handling the matter that many game theorists have found worthy of detailed pursuit. This involves the computation of equilibria in beliefs.
In fact, the behaviorist needs the concept of equilibrium in beliefs too, but for different purposes. As we've seen, the concept of NE sometimes doesn't go deep enough as an analytical instrument to tell us all that we think might be important in a game. Thus even behaviorists who aren't impressed with the project of refinements make frequent use of the concept of subgame-perfect equilibrium (SPE) as discussed in Section 2.6. But now consider the three-player imperfect-information game below (taken from Kreps (1990), p. 426):
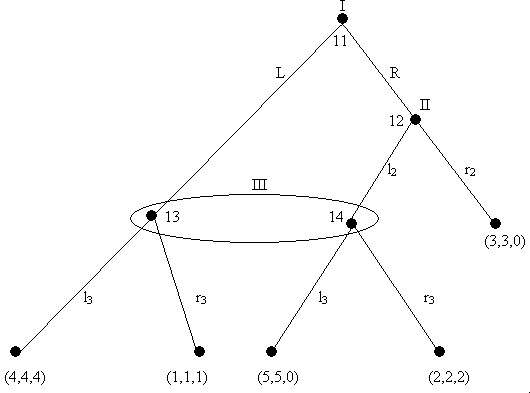
Figure 13
One of the NE of this game is Lr2l3. This is because if Player I plays L, then Player II playing r2 has no incentive to change strategies because her only node of action, 12, is off the path of play. But this NE seems to be purely technical; it makes little sense as a solution. This reveals itself in the fact that if the game beginning at node 14 could be treated as a subgame, Lr2l3 would not be an SPE. Whenever she does get a move, Player II should play l2. But if Player II is playing l2 then Player I should switch to R. In that case Player III should switch to r3, sending Player II back to r2. And here's a new, ‘sensible’, NE: Rr2r3. I and II in effect play ‘keepaway’ from III; and so that's what we'll name this game.
This NE is ‘sensible’ in just the same way that a SPE outcome in a perfect-information game is more sensible than other non-SPE NE. However, we can't select it by applying Zermelo's algorithm. Because nodes 13 and 14 fall inside a common information set, Keepaway has only one subgame (namely, the whole game). We need a ‘cousin’ concept to SPE that we can apply in cases of imperfect information, and we need a new solution procedure to replace Zermelo's algorithm for such games.
Notice what Player III in Keepaway is wondering about as he selects his strategy. "Given that I get a move," he asks himself, "was my action node reached from node 11 or from node 12?" What, in other words, are the conditional probabilities that III is at node 13 or 14 given that he has a move? Now, if conditional probabilities are what III wonders about, then what Players I and II must make conjectures about when they select their strategies are III's beliefs about these conditional probabilities. In that case, I must conjecture about II's beliefs about III's beliefs, and III's beliefs about II's beliefs and so on. The relevant beliefs here are not merely strategic, as before, since they are not just about what players will do given a set of payoffs and game structures, but about what they think makes sense given some understanding or other of conditional probability.
What beliefs about conditional probability is it reasonable for players to expect from each other? The normative theorist might insist on whatever the best mathematicians have discovered about the subject. Clearly, however, if this is applied then a theory of games that incorporated it would not be descriptively true of most people. The behaviorist will insist on imposing only behavioral habits that a process of natural selection might build into its products. Perhaps some actual or possible creatures might observe habits that respect Bayes's rule, which is the minimal true generalization about conditional probability that an agent could know if it knows any such generalizations at all. Adding more sophisticated knowledge about conditional probability amounts to refining the concept of equilibrium-in-belief, just as some game theorists like to refine NE. You can imagine what behaviorists think of that project!
Here, we will restrict our attention to the least refined equilibrium-in-belief concept, that obtained when we require players to reason in accordance with Bayes's rule. Bayes's rule tells us how to compute the probability of an event F given information E (written ‘pr(F/E)’):
pr(F/E) = [pr(E/F) X pr(F)] / pr(E)
We will henceforth assume that players do not hold beliefs inconsistent with this equality.
We may now define a sequential equilibrium. A SE has two parts: (1) a strategy profile § for each player, as before, and (2) a system of beliefs μ for each player. μ assigns to each information set h a probability distribution over the nodes x in h, with the interpretation that these are the beliefs of player i(h) about where in his information set he is, given that information set h has been reached. Then a sequential equilibrium is a profile of strategies § and a system of beliefs μ consistent with Bayes's rule such that starting from every information set h in the tree player i(h) plays optimally from then on, given that what he believes to have transpired previously is given by μ(h) and what will transpire at subsequent moves is given by §.
We now demonstrate the concept by application to Keepaway. Consider again the uninteresting NE Lr2l3. Suppose that Player III assigns pr(1) to her belief that if she gets a move she is at node 13. Then Player II, given a consistent μ(II), must believe that III will play l3, in which case her only SE strategy is l2. So although Lr2l3 is a NE, it is not a SE. This is of course what we want.
The use of the consistency requirement in this example is somewhat trivial, so consider now a second case (also taken from Kreps (1990), p. 429):
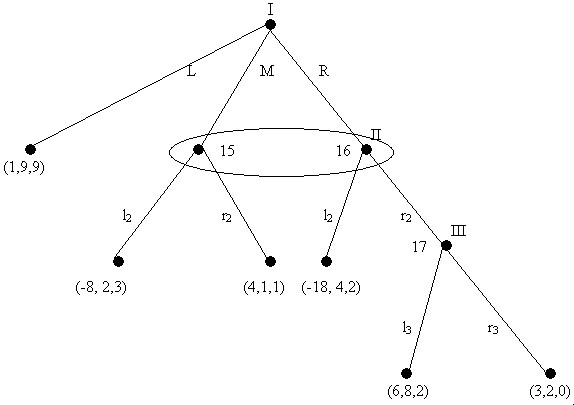
Figure 14
Suppose that I plays L, II plays l2 and III plays l3. Suppose also that μ(II) assigns pr(.3) to node 16. In that case, l2 is not a SE strategy for II, since l2 returns an expected payoff of .3(4) + .7(2) = 2.6, while r2 brings an expected payoff of 3.1. Notice that if we fiddle the strategy profile for player III while leaving everything else fixed, l2 could become a SE strategy for II. If §(III) yielded a play of l3 with pr(.5) and r3 with pr(.5), then if II plays r2 his expected payoff would now be 2.2, so Ll2l3 would be a SE. Now imagine setting μ(III) back as it was, but change μ(II) so that II thinks the conditional probability of being at node 16 is greater than .5; in that case, l2 is again not a SE strategy.
The idea of SE is hopefully now clear. We can apply it to the river-crossing game in a way that avoids the necessity for the hunter to flip any coins of we modify the game a bit. Suppose now that II can change bridges twice during the fugitive's passage, and will catch him just in case she meets him as he leaves the bridge. Then the hunter's SE strategy is to divide her time at the three bridges in accordance with the proportion given by the equation in the third paragraph of Section 3 above.
It must be noted that since Bayes's rule cannot be applied to events with probability 0, its application to SE requires that players assign non-zero probabilities to all actions available in trees. This requirement is captured by supposing that all strategy profiles be strictly mixed, that is, that every action at every information set be taken with positive probability. You will see that this is just equivalent to supposing that all hands sometimes tremble. A SE is said to be trembling-hand perfect if all strategies played at equilibrium are best replies to strategies that are strictly mixed. You should also not be surprised to be told that no weakly dominated strategy can be trembling-hand perfect, since the possibility of trembling hands gives players the most persuasive reason for avoiding such strategies.
We've seen that in the one-shot PD the only NE is mutual defection. This may no longer hold, however, if the players expect to meet each other again in future PDs. Imagine that four firms, all making widgets, agree to maintain high prices by jointly restricting supply. (That is, they form a cartel.) This will only work if each firm maintains its agreed production quota. Typically, each firm can maximize its profit by departing from its quota while the others observe theirs, since it then sells more units at the higher market price brought about by the almost-intact cartel. In the one-shot case, all firms would share this incentive to defect and the cartel would immediately collapse. However, the firms expect to face each other in competition for a long period. In this case, each firm knows that if it breaks the cartel agreement, the others can punish it by underpricing it for a period long enough to more than eliminate its short-term gain. Of course, the punishing firms will take short-term losses too during their period of underpricing. But these losses may be worth taking if they serve to reestablish the cartel and bring about maximum long-term prices.
One simple, and famous (but not, contrary to widespread myth, necessarily optimal) strategy for preserving cooperation in repeated PDs is called tit-for-tat. This strategy tells each player to behave as follows:
There are two complications. First, the players must be uncertain as to when their interaction ends. Suppose the players know when the last round comes. In that round, it will be rational for players to defect, since no punishment will be possible. Now consider the second-last round. In this round, players also face no punishment for defection, since they know they will defect in the last round anyway. So they defect in the second-last round. But this means they face no threat of punishment in the third-last round, and defect there too. We can simply iterate this backwards through the game tree until we reach the first round. Since cooperation is not rational in that round, tit-for-tat is no longer a rational strategy, and we get the same outcome -- mutual defection -- as in the one-shot PD. Therefore, cooperation is only possible in repeated PDs where the expected number of repetitions is indeterminate. (Of course, this does apply to many real-life games.)
But now we introduce a second complication. Suppose that players' ability to distinguish defection from cooperation is imperfect. Consider our case of the widget cartel. Suppose the players observe a fall in the market price of widgets. Perhaps this is because a cartel member cheated. Or perhaps it has resulted from an exogenous drop in demand. If tit-for-tat players mistake the second case for the first, they will defect, thereby setting off a chain-reaction of mutual defections from which they can never recover, since every player will reply to the first encountered defection with defection, thereby begetting further defections, and so on.
If players know that such miscommunication is possible, they must resort to more sophisticated strategies. In particular, they must be prepared to sometimes risk following defections with cooperation in order to test their inferences. However, they mustn't be too forgiving, lest other players find it rationally optimal to exploit them through deliberate defections. In general, sophisticated strategies have a problem. Because they are more difficult for other players to infer, their use increases the probability of miscommunication. But miscommunication is what causes repeated-game cooperative equilibria to unravel in the first place! The moral of this is that PDs, even repeated ones, are very difficult to escape from. Rational players do best trying to avoid situations that are PDs, rather than relying on cunning strategems for trying to get out of them.
Real, complex, social and political dramas are seldom straightforward instantiations of simple games such as PDs. Russell Hardin (1995) offers an analysis of two recent, very real (and very tragic) political cases, the Yugoslavian civil war of 1991-95, and the 1994 Rwandan genocide, as PDs that were nested inside coordination games. A coordination game occurs whenever the utility of two or more players is maximized by their doing the same thing, and where such correspondence is more important to them than what, in particular, they both do. A standard example arises with rules of the road: ‘All drive on the left’ and ‘All drive on the right’ are both outcomes that are NEs, and neither is more efficient than the other. In games of ‘pure’ coordination, it doesn't even help to use more selective equilibrium criteria. For example, suppose that we require our players to reason in accordance with Bayes's rule (see Section 3 above). In these circumstances, any strategy that is a best reply to any vector of mixed strategies available in NE is said to be rationalizable. That is, a player can find a set of systems of beliefs for the other players such that any history of the game along an equilibrium path is consistent with that set of systems. Pure coordination games are characterized by non-unique vectors of rationalizable strategies. In such situations, players may try to predict equilibria by searching for focal points, that is, features of some strategies that they believe will be salient to other players, and that they believe other players will believe to be salient to them. Unfortunately, in many of the social and political games played by people (and some other animals), the biologically shallow properties by which people sort themselves into racial and ethnic groups serve highly efficiently as such features. Hardin's analysis of recent genocides relies on this fact.
According to Hardin, neither the Yugolslavian nor the Rwandan disasters were PDs to begin with. That is, in neither situation, on either side, did most people begin by preferring the destruction of the other to mutual cooperation. However, the deadly logic of coordination, deliberately abetted by self-serving politicians, dynamically created PDs. Some individual Serbs (Hutus) were encouraged to perceive their individual interests as best served through identification with Serbian (Hutu) group-interests. That is, they found that some of their circumstances, such as those involving competition for jobs, had the form of coordination games. They thus acted so as to create situations in which this was true for other Serbs (Hutus) as well. Eventually, once enough Serbs (Hutus) identified self-interest with group-interest, the identification became almost universally correct, because (1) the most important goal for each Serb (Hutu) was to do roughly what every other Serb (Hutu) would, and (2) the most distinctively Serbian thing to do, the doing of which permitted coordination, was to exclude Croats (Tutsi). That is, strategies involving such exclusionary behavior were selected as a result of having efficient focal points. This situation made it the case that an individual -- and individually threatened -- Croat's (Tutsi's) self-interest was best maximized by coordinating on assertive Croat (Tutsi) group-identity, which further increased pressures on Serbs (Hutus) to coordinate, and so on. Note that it is not an aspect of this analysis to suggest that Serbs or Hutus started things; the process could have been (even if it wasn't in fact) perfectly reciprocal. But the outcome is ghastly: Serbs and Croats (Hutus and Tutsis) seem progressively more threatening to each other as they rally together for self-defense, until both see it as imperative to preempt their rivals and strike before being struck. If Hardin is right -- and the point here is not to claim that he is, but rather to point out the worldly importance of determining which games agents are in fact playing -- then the mere presence of an external enforcer (NATO?) would not have changed the game, pace the Hobbesian analysis, since the enforcer could not have threatened either side with anything worse than what each feared from the other. What was needed was recalibration of evaluations of interests, which (arguably) happened in Yugoslavia when the Croatian army began to decisively win, at which point Bosnian Serbs decided that their self/group interests were best served by the arrival of NATO peacekeepers. The Rwandan conflict, meanwhile, drags on in the neighbouring country (the Congo) to which military and political developments have shifted it.
Of course, it is not the case that most repeated games lead to disasters. The biological basis of friendship in people and other animals is probably partly a function of the logic of repeated games. The importance of payoffs achievable through cooperation in future games leads those who expect to interact in them to be less selfish than temptation would suggest in present games. Furthermore, cultivating shared interests and sentiments provides networks of focal points around which coordination can be facilitated.
Consider the following hypothetical example (which is not a PD). Suppose you own a piece of land adjacent to mine, and I'd like to buy it so as to expand my lot. Unfortunately, you don't want to sell at the price I'm willing to pay. If we move simultaneously -- you post a selling price and I independently give my agent an asking price -- there will be no sale. So I might try to change your incentives by playing an opening move in which I announce that I'll build a putrid-smelling sewage disposal plant on my land beside yours unless you sell, thereby lowering your price. I've now turned this into a sequential-move game. However, this move so far changes nothing. If you refuse to sell in the face of my threat, it is then not in my interest to carry it out, because in damaging you I also damage myself. Since you know this you should ignore my threat. My threat is incredible, a case of cheap talk.
However, I could make my threat credible by committing myself. I could sign a contract with some farmers promising to supply them with treated sewage (fertilizer) from my plant, but including an escape clause in the contract releasing me from my obligation only if I can double my lot size and so put it to some other use. Now my threat is credible: if you don't sell, I'm committed to building the sewage plant. Since you know this, you now have an incentive to sell me your land in order to escape its ruination.
This sort of case exposes one of many fundamental differences between the logic of non-parametric and parametric maximization. In parametric situations, an agent can never be made worse off by having more options. But where circumstances are non-parametric, one agent's strategy can be influenced in another's favour if options are visibly restricted. Cortez's burning of his boats (see Section 1) is, of course, an instance of this, one which serves to make the usual metaphor literal.
Another example will illustrate this, as well as the applicability of principles across game-types. Here we will build an imaginary situation that is not a PD -- since only one player has an incentive to defect -- but which is a social dilemma insofar as its NE in the absence of commitment is Pareto-inferior to an outcome that is achievable with a commitment device. Suppose that two of us wish to poach a rare antelope from a national park in order to sell the trophy. One of us must flush the animal down towards the second person, who waits in a blind to shoot it and load it onto a truck. You promise, of course, to share the proceeds with me. However, your promise is not credible. Once you've got the buck, you have no reason not to drive it away and pocket the full value from it. After all, I can't very well complain to the police without getting myself arrested too. But now suppose I add the following opening move to the game. Before our hunt, I rig out the truck with an alarm that can be turned off only by punching in a code. Only I know the code. If you try to drive off without me, the alarm will sound and we'll both get caught. You, knowing this, now have an incentive to wait for me. What is crucial to notice here is that you prefer that I rig up the alarm, since this makes your promise to give me my share credible. If I don't do this, leaving your promise incredible, we'll be unable to agree to try the crime in the first place, and both of us will lose our shot at the profit from selling the trophy. Thus, you benefit from my binding you.
We may now combine our analysis of PDs and commitment devices in discussion of the application that first made game theory famous outside of the academic community. The nuclear stand-off between the superpowers during the Cold War was exhaustively studied by the first generation of game theorists, many of whom worked for the US military. (See Poundstone 1992 for historical details.) Both the USA and the USSR maintained the following policy. If one side launched a first strike, the other threatened to answer with a devastating counter-strike. This pair of reciprocal strategies, which by the late 1960s would effectively have meant blowing up the world, was known as ‘Mutually Assured Destruction’, or ‘MAD’. Game theorists objected that MAD was mad, because it set up a Prisoner's Dilemma as a result of the fact that the reciprocal threats were incredible. Suppose the USSR launches a first strike against the USA. At that point, the American President faces the following situation. His country is already destroyed. He doesn't bring it back to life by now blowing up the world, so he has no incentive to carry out his threat, which has now manifestly failed to achieve its point. Since the Russians know this, they should ignore the threat and strike first! Of course, the Americans are in exactly the same position. Each power will recognize this incentive on the part of the other, and so will anticipate an attack if they don't preempt it. What we should therefore expect, because it is the only NE of the game, is a race between the two powers to be the first to attack.
This game-theoretic analysis caused genuine consternation and fear on both sides during the Cold War, and produced some rather bizarre attempts at setting up strategic commitment devices. President Nixon, for example, had the CIA try to convince the Russians that he was insane, so that they'd believe that he'd launch a retaliatory strike even when it was no longer in his interest to do so. Similarly, the Soviet KGB leaked fabricated medical reports exaggerating Brezhnev's senility with the same end in mind. Ultimately, the Americans broke this deadly symmetry by using a ‘doomsday device’. They equipped a worldwide fleet of submarines with enough missiles to destroy the USSR, and arranged their communications technology in such a way that the President could not be sure to be able to reach the submarines and cancel their orders to attack if any Soviet missile crossed the radar ‘trigger line’. Of course, this strategy depended on making sure that the Russians were aware of the device. In Stanley Kubrick's classic film Dr. Strangelove, the world is destroyed by accident because the Russians build a doomsday machine but then keep it a secret! As a result, when a mad American colonel launches missiles at Russia on his own accord, and the American President tries to convince his Soviet counterpart that the attack was unintended, the Russian President sheepishly tells him about the secret doomsday machine. Now the two Presidents can do nothing but watch in dismay as the world is blown up -- due to a game-theoretic mistake.
Commitment can sometimes be secured through the value to a player of her own reputation. For example, a government tempted to negotiate with terrorists to secure the release of hostages on a particular occasion may commit to a ‘line in the sand’ strategy for the sake of maintaining a reputation for toughness intended to reduce terrorists' incentives to launch future attacks. A different sort of example is provided by Qantas Airlines of Australia. Qantas has never suffered an accident, and makes much of this in its advertising. This means that its planes probably are safer than average even if the initial advantage was merely a statistical artifact, because the value of its ability to claim a perfect record rises the longer it lasts, and so gives the airline continuous incentives to incur greater costs in safety assurance.
Certain conditions must hold if reputation effects are to underwrite commitment. First, the game must be repeated, with uncertainty as to which round is the last one. The repeated PD can be used to illustrate the importance of this principle. Cooperation can be the dominant strategy in a repeated PD because a player can gain more from his reputation for cooperation, through inducing expectations of cooperation in others, than he can gain through defection in a single round. However, if the players know in advance which round will be their last, this equilibrium unravels. In the last round reputation no longer has a value, and so both players will defect. In the second-last round, the players know they will defect in the last round, so reputation becomes worthless here too and they will again defect. This makes reputation worthless in the third-last round, and so on. The process iterates back to the first round, so no cooperation ever occurs. This point can be generalized to state the most basic condition on the possibility for using reputation effects as commitment devices: the value of the reputation must be greater to its cultivator than the value to him of sacrificing it in any particular round. Thus players may establish commitment by reducing the value of each round so that the temptation to defect in any round never gets high enough to make it rational. For example, parties to a contract may exchange their obligations in small increments to reduce incentives on both sides to renege. Thus builders in construction projects may be paid in weekly or monthly installments. Similarly, the International Monetary Fund often dispenses loans to governments in small tranches, thereby reducing governments' incentives to violate loan conditions once the money is in hand; and governments may actually prefer such arrangements in order to remove domestic political pressure for non-compliant use.
In 1969, for example, the philosopher David Lewis (1969) published Convention, in which the conceptual framework of game-theory was applied to one of the fundamental issues of twentieth-century epistemology, the nature and extent of conventions governing semantics and their relationship to the justification of propositional beliefs. This book stands as one of the classics of analytic philosophy, and its stock is presently rising still further as we become more aware of the significance of the trail it blazed. The basic insight can be captured using a simple example. The word ‘chicken’ denotes chickens and ‘ostrich’ denotes ostriches. We would not be better or worse off if ‘chicken’ denoted ostriches and ‘ostrich’ denoted chickens; however, we would be worse off if half of us used the pair of words the first way and half the second, or if all of us randomized between them to refer to flightless birds generally. This insight, of course, well preceded Lewis; but what he recognized is that this situation has the logical form of a coordination game. Thus, while particular conventions may be arbitrary, the interactive structures that stabilize and maintain them are not. Furthermore, the equilibria involved in coordinating on noun-meanings appear to have an arbitrary element only because we cannot Pareto-rank them; but Millikan (1984) shows implicitly that in this respect they are atypical of linguistic coordinations. In general, the various NE in coordination games can very often be ranked. Ross & LaCasse (1995) present the following example. In a city, drivers must coordinate on one of two NE with respect to their behaviour at traffic lights. Either all must rush yellows and pause on shifts to green, or slow down on yellows and jump forward on shifts to green. Both patterns are NE, in that once a community has coordinated on one of them no individual has an incentive to deviate: those who slow down on yellows while others are rushing them will get rear-ended, while those who rush yellows in the other equilibrium will risk collision with those who jump forward quickly on greens. Therefore, once a city's traffic pattern settles on one of these equilibria it will tend to stay there. However, the two states are not Pareto-indifferent, since the second NE allows more cars to turn left on each cycle (in a right-hand-drive jurisdiction), which reduces the extent of bottlenecks and allows all drivers to expect greater efficiency in getting about. Conventions on standards of evidence and rationality are likely to be of this character. While various arrangements might be NE in the social game of science, as followers of Thomas Kuhn like to remind us, it is highly improbable that all of these lie on a single Pareto-indifference curve. These themes, strongly represented in contemporary epistemology, philosophy of science and philosophy of language, are all bequests of game theory by way (at least indirectly) of Lewis. (The reader can find a broad sample of applications, and references to the large literature, in Nozick (1998).) However, Lewis restricted his attention to static game theory, in which agents choose strategies given exogenously fixed utility-functions. As a result of this restriction, his account is able to show us why conventions are important and stable, but it invites a difficult and perhaps ultimately fruitless quest for a general theory of rationality. This is because, as we saw in Section 3 above, in coordination (and other) games with multiple NE, what counts as a solution is highly sensitive to conjectures made by players about one another's beliefs and computational ability. This has excited a good deal of attention, especially from philosophers, on the implications of many subtle variations in the norms of strategic rationality. However, if game theory is to explain actual, natural behavior and its history in the way suggested by Gintis (2000) above, then we need some account of what is attractive about equilibria in games even when no analysts or rational calculators are around to identify them. To make reference again to Lewis's topic, when human language developed there was no external referee to care about and arrange for Pareto-efficiency. In order to understand Gintis's optimism about the reach of game theory, we must therefore extend our attention to evolutionary games.
Game theory has been fruitfully applied in evolutionary biology, where species and/or genes are treated as players, since pioneering work by Maynard Smith (1982) and his collaborators. Evolutionary (or dynamic) game theory now constitutes a significant new mathematical extension applicable to many settings apart from the biological. Thus Skyrms (1996) uses evolutionary game theory to try to answer questions Lewis could not even ask, about the conditions under which language, concepts of justice, the notion of private property, and other non-designed, general phenomena of interest to philosophers would be likely to arise. What is novel about evolutionary game theory is that moves are not chosen by rational agents. Instead, agents are typically hard-wired with particular strategies, and success for a strategy is defined in terms of the number of copies that a strategy will leave of itself to play in the games of succeeding generations. The strategies themselves are therefore the players, and the games they play are dynamic rather than static.
The discussion here will closely follow Skyrms's. We begin by introducing the replicator dynamics. Consider first how natural selection works to change lineages of animals, modifying, creating and destroying species. The basic mechanism is differential reproduction. Any animal with heritable features that increase its expected number of offspring in a given environment will tend to leave more offspring than others so long as the environment remains relatively stable. These offspring will be more likely to inherit the features in question. Therefore, the proportion of these features in the population will gradually increase as generations pass. Some of these features may go to fixation, that is, eventually take over the entire population (until the environment changes).
How does game theory enter into this? Often, one of the most important aspects of an organism's environment will be the behavioural tendencies of other organisms. We can think of each lineage as ‘trying’ to maximize its reproductive fitness (= expected number of grandchildren) through finding strategies that are optimal given the strategies of other lineages. So evolutionary theory is another domain of application for non-parametric analysis.
In dynamic game theory, we no longer think of individuals as choosing strategies as they move from one game to another. This is because our interests are different. We're now concerned less with finding the equilibria of single games than with discovering which equilibria are stable, and how they will change over time. So we now model the strategies themselves as playing against each other. One strategy is ‘better’ than another if it is likely to leave more copies of itself in the next generation, when the game will be played again. We study the changes in distribution of strategies in the population as the sequence of games unfolds.
For dynamic game theory, we introduce a new equilibrium concept, due to Maynard Smith (1982). A set of strategies, in some particular proportion (e.g., 1/3:2/3, 1/2:1/2, 1/9:8/9, 1/3:1/3:1/6:1/6 -- always summing to 1) is at an ESS (Evolutionary Stable Strategy) equilibrium just in case (1) no individual playing one strategy could improve its reproductive fitness by switching to one of the other strategies in the proportion, and (2) no mutant playing a different strategy altogether could establish itself (‘invade’) in the population.
The principles of evolutionary game theory are best explained through examples. Skyrms begins by investigating the conditions under which a sense of justice -- understood as a disposition to view equal divisions of resources as fair unless efficiency considerations suggest otherwise in special cases -- might arise. He asks us to consider a population in which individuals regularly meet each other and must bargain over resources. Begin with three types of individuals:
We refer to equilibria in which more than one strategy occurs as polymorphisms. In general, in Skyrms's game, any polymorphism in which Greedy demands x and Modest demands 1-x is an ESS. The question that interests the student of justice concerns the relative likelihood with which these different equilibria arise.
This depends entirely on the proportions of strategies in the original population state. If the population begins with more than one Fairman, then there is some probability that Fairmen will encounter each other, and get the highest possible average payoff. Modests by themselves do not inhibit the spread of Fairmen; only Greedies do. But Greedies themselves depend on having Modests around in order to be viable. So the more Fairmen there are in the population relative to pairs of Greedies and Modests, the better Fairmen do on average. This implies a threshold effect. If the proportion of Fairmen drops below 33%, then the tendency will be for them to fall to extinction because they don't meet each other often enough. If the population of Fairmen rises above 33%, then the tendency will be for them to rise to fixation because their extra gains when they meet each other compensates for their losses when they meet Greedies. You can see this by noticing that when each strategy is used by 33% of the population, all have an expected average payoff of 1/3. Therefore, any rise above this threshold on the part of Fairmen will tend to push them towards fixation.
This result shows that and how, given certain relatively general conditions, justice as we have defined it can arise dynamically. The news for the fans of justice gets more cheerful still if we introduce correlated play.
The model we just considered assumes that strategies are not correlated, that is, that the probability with which every strategy meets every other strategy is a simple function of their relative frequencies in the population. We now examine what happens in our dynamic resource-division game when we introduce correlation. Suppose that Fairmen have a slight ability to distinguish and seek out other Fairmen as interaction partners. In that case, Fairmen on average do better, and this must have the effect of lowering their threshold for going to fixation.
A dynamic-game modeler studies the effects of correlation and other parametric constraints by means of running large computer simulations in which the strategies compete with one another, round after round, in the virtual environment. The starting proportions of strategies, and any chosen degree of correlation, can simply be set in the programme. One can then watch its dynamics unfold over time, and measure the proportion of time it stays in any one equilibrium. These proportions are represented by the relative sizes of the basins of attraction for different possible equilibria. Equilibria are attractor points in a dynamic space; a basin of attraction for each such point is then the set of points in the space from which the population will converge to the equilibrium in question.
In introducing correlation into his model, Skyrms first sets the degree of correlation at a very small .1. This causes the basin of attraction for equilibrium (i) to shrink by half. When the degree of correlation is set to .2, the polymorphic basin reduces to the point at which the population starts in the polymorphism. Thus very small increases in correlation produce large proportionate increases in the stability of the equilibrium where everyone plays Fairman. A small amount of correlation is a reasonable assumption in most populations, given that neighbours tend to interact with one another and to mimic one another (either genetically or because of tendencies to deliberately copy each other), and because genetically similar animals are more likely to live in common environments. Thus if justice can arise at all it will tend to be dominant and stable.
Much of political philosophy consists in attempts to produce deductive normative arguments intended to convince an unjust agent that she has reasons to act justly. Skyrms's analysis suggests a quite different approach. Fairman will do best of all in the dynamic game if he takes active steps to preserve correlation. Therefore, there is evolutionary pressure for both moral approval of justice and just institutions to arise. Most people may think that 50-50 splits are ‘fair’, and worth maintaining by moral and institutional reward and sanction, because we are the products of a dynamic game that promoted our tendency to think this way.
The topic that has received most attention from evolutionary game theorists is altruism, defined as any behaviour by an organism that decreases its own expected fitness in a single interaction but increases that of the other interactor. It is common in nature. How can it arise, however, given Darwinian competition?
Skyrms studies this question using the dynamic Prisoner's Dilemma as his example. This is simply a series of PD games played in a population, some of whose members are defectors and some of whom are cooperators. Payoffs, as always in dynamic games, are measured in terms of expected numbers of copies of each strategy in future generations.
Let U(A) be the average fitness of strategy A in the population. Let U be the average fitness of the whole population. Then the proportion of strategy A in the next generation is just the ratio U(A)/U. So if A has greater fitness than the population average A increases. If A has lower fitness than the population average then A decreases.
In the dynamic PD where interaction is random (i.e., there's no correlation), defectors do better than the population average as long as there are cooperators around. This follows from the fact that, as we saw in Section 2.4, defection is always the dominant strategy in a single game. 100% defection is therefore the ESS in the dynamic game without correlation, corresponding to the NE in the one-shot static PD.
However, introducing the possibility of correlation radically changes the picture. We now need to compute the average fitness of a strategy given its probability of meeting each other possible strategy. In the dynamic PD, cooperators whose probability of meeting other cooperators is high do better than defectors whose probability of meeting other defectors is high. Correlation thus favours cooperation.
In order to be able to say something more precise about this relationship between correlation and cooperation (and in order to be able to relate evolutionary game theory to issues in decision theory, a matter falling outside the scope of this article), Skyrms introduces a new technical concept. He calls a strategy adaptively ratifiable if there is a region around its fixation point in the dynamic space such that from anywhere within that region it will go to fixation. In the dynamic PD, both defection and cooperation are adaptively ratifiable. The relative sizes of basins of attraction are highly sensitive to the particular mechanisms by which correlation is achieved. To illustrate this point, Skyrms builds several examples.
One of Skyrms's models introduces correlation by means of a filter on pairing for interaction. Suppose that in round 1 of a dynamic PD individuals inspect each other and interact, or not, depending on what they find. In the second and subsequent rounds, all individuals who didn't pair in round 1 are randomly paired. In this game, the basin of attraction for defection is large unless there is a high proportion of cooperators in round one. In this case, defectors fail to pair in round 1, then get paired mostly with each other in round 2 and drive each other to extinction. A model which is more interesting, because its mechanism is less artificial, does not allow individuals to choose their partners, but requires them to interact with those closest to them. Because of genetic relatedness (or cultural learning by copying) individuals are more likely to resemble their neighbours than not. If this (finite) population is arrayed along one dimension (i.e., along a line), and both cooperators and defectors are introduced into positions along it at random, then we get the following dynamics. Isolated cooperators have lower expected fitness than the surrounding defectors and are driven locally to extinction. Members of groups of two cooperators have a 50% probability of interacting with each other, and a 50% probability of each interacting with a defector. As a result, their average expected fitness remains smaller than that of their neighbouring defectors, and they too face probable extinction. Groups of three cooperators form an unstable point from which both extinction and expansion are equally likely. However, in groups of four or more cooperators at least one encounter of a cooperator with a cooperator sufficient to at least replace the original group is guaranteed. Under this circumstance, the cooperators as a group do better than the surrounding defectors and increase at their expense. Eventually cooperators go almost to fixation -- but nor quite. Single defectors on the periphery of the population prey on the cooperators at the ends and survive as little ‘criminal communities’. We thus see that altruism can not only be maintained by the dynamics of evolutionary games, but, with correlation, can even spread and colonize originally non-altruistic populations.
Darwinian dynamics thus offers qualified good news for cooperation. Notice, however, that this holds only so long as individuals are stuck with their natural or cultural programming and can't re-evaluate their utilities for themselves. If our agents get too smart and flexible, they may notice that they're in PDs and would each be best off defecting. In that case, they'll eventually drive themselves to extinction - unless they develop stable, and effective, moral norms that work to reinforce cooperation. But, of course, these are just what we would expect to evolve in populations of animals whose average fitness levels are closely linked to their capacities for successful social cooperation. Even given this, these populations will go extinct unless they care about future generations for some reason. But there's no rational reason as to why agents should care about future generations if each new generation wholly replaces the preceding one at each change of cohorts. For this reason, economists use ‘overlapping generations’ models when modeling distribution games. Individuals in generation 1 who will last until generation 5 save resources for the generation 3 individuals with whom they'll want to cooperate; and by generation 3 the new individuals care about generation 6; and so on.
An enormous range of further applications of both static and dynamic game theory have been developed, but we have perhaps now provided enough to convince the reader of the tremendous utility of this analytical tool. The reader whose appetite for more has been thoroughly aroused should find that she now has sufficient grasp of fundamentals to be able to work through the large literature, of which some highlights are listed below.
Game theory has countless applications, of which this article has been able to suggest only a few. Readers in search of more, but not wishing to immerse themselves in mathematics, can find a number of good sources. Dixit and Nalebuff (1991) is especially strong on political and social examples. McMillan (1991) emphasizes business applications. The great historical breakthrough is von Neumann and Morgenstern (1947), which those with scholarly interest in game theory should read with classic papers of John Nash (1950a, 1950b, 1951). For a contemporary mathematical treatment that is unusually philosophically sophisticated, Binmore (1992) (**) is in a class by itself. The second half of Kreps (1990) (**) is the best available starting point for a tour of the philosophical worries surrounding equilibrium selection for non-behaviorists. Koons (1992) takes these issues further. Fudenberg and Tirole (1991) is the most thorough and complete mathematical text available. Gintis (2000) (**) has provided a new text crammed with terrific problem exercises, which is also unique in that it treats evolutionary game theory as providing the foundational basis for game theory in general. This likely represents the wave of the future. Recent developments in fundamental theory are well represented in Binmore, Kirman and Tani (1993).
The philosophical foundations of the basic game-theoretic concepts as economists understand them are presented in LaCasse and Ross (1994). Ross and LaCasse (1995) outline the relationships between games and the axiomatic assumptions of microeconomics and macroeconomics. Philosophical puzzles at this foundational level are critically discussed in Bicchieri (1993) (**). Lewis (1969) (**) puts game-theoretic equilibrium concepts to wider application in philosophy, a program that is carried a good deal further in Skyrms (1996) (**). (See also Nozick [1998].) Gauthier (1986) launches a literature not surveyed in this article, in which the possibility of game-theoretic foundations for contractarian ethics is investigated. This work is critically surveyed in Vallentyne (1991), and extended into a dynamic setting in Danielson (1992). Binmore (1994, 1998) (**), however, effectively demolishes this project. Philosophers will also find Hollis (1998) to be of interest.
Hardin (1995) is one of many examples of the application of game theory to problems in applied political theory. Baird, Gertner and Picker (1994) review uses of game theory in legal theory and jurisprudence. Mueller (1997) surveys applications in political economy. Ghemawat (1997) does the same in business strategy. Poundstone (1992) provides a lively history of the Prisoner's Dilemma and its use by Cold War strategists. Durlauf and Young (2001) is a good collection on applications to social structures and social change.
Evolutionary game theory owes its explicit genesis to Maynard Smith (1982) (**). For a text that integrates game theory directly with biology, see Sigmund (1993). The most exciting applications of evolutionary game theory to a range of philosophical issues, on which this article has drawn heavily, is Skyrms (1996) (**). These issues and others are critically discussed from various angles in Danielson (1998). Mathematical foundations for dynamic games are presented in Weibull (1995), and pursued further in Samuelson (1997) and Fudenberg and Levine (1998). As noted above, Gintis (2000) (**) now provides an introductory textbook that takes evolutionary modeling to be foundational to all of game theory. Many philosophers will also be interested in Binmore (1994, 1998) (**), which shows that application of game-theoretic analysis can underwrite a loosely Rawlsian theory of justice that does not require recourse to Kantian presuppositions about what rational agents would desire behind a veil of ignorance concerning their identities and social roles. (In addition, Binmore offers excusions into a vast range of other issues both central and peripheral to both the foundations and the frontiers of game theory; these books are a tour de force.) And almost everyone will be interested in Frank (1988) (**), where evolutionary game theory is used to illuminate basic features of human nature and emotion.
| Don Ross University of Cape Town/University of Alabama at Birmingham dross@commerce.uct.ac.za |
A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z