Stanford Encyclopedia of Philosophy
This is a file in the archives of the Stanford Encyclopedia of Philosophy.

The Axiom of Choice

First published Tue Jan 8, 2008; substantive revision Wed Jan 9, 2008

The principle of set theory known as the Axiom of Choice has been hailed as “probably the most interesting and, in spite of its late appearance, the most discussed axiom of mathematics, second only to Euclid's axiom of parallels which was introduced more than two thousand years ago” (Fraenkel, Bar-Hillel & Levy 1973, §II.4). The fulsomeness of this description might lead those unfamiliar with the axiom to expect it to be as startling as, say, the Principle of the Constancy of the Velocity of Light or the Heisenberg Uncertainty Principle. But in fact the Axiom of Choice as it is usually stated appears humdrum, even self-evident. For it amounts to nothing more than the claim that, given any collection of mutually disjoint nonempty sets, it is possible to assemble a new set — a transversal or choice set — containing exactly one element from each member of the given collection. Nevertheless, this seemingly innocuous principle has far-reaching mathematical consequences — many indispensable, some startling — and has come to figure prominently in discussions on the foundations of mathematics. It (or its equivalents) have been employed in countless mathematical papers, and a number of monographs have been exclusively devoted to it.

1. Origins and Chronology of the Axiom of Choice

In 1904 Ernst Zermelo formulated the Axiom of Choice (abbreviated as AC throughout this article) in terms of what he called coverings (Zermelo 1904). He starts with an arbitrary set M and uses the symbol M′ to denote an arbitrary nonempty subset of M, the collection of which he denotes by M. He continues:

Imagine that with every subset M′ there is associated an arbitrary element m1′, that occurs in M′ itself; let m1′ be called the “distinguished” element of M′. This yields a “covering” g of the set M by certain elements of the set M. The number of these coverings is equal to the product [of the cardinalities of all the subsets M′] and is certainly different from 0.

The last sentence of this quotation — which asserts, in effect, that coverings always exist for the collection of nonempty subsets of any (nonempty) set — is Zermelo's first formulation of the Axiom of Choice[1]. This is now usually stated in terms of choice functions: here a choice function on a collection H of nonempty sets is a map f with domain H such that f(X) ∈ X for every X ∈ H.

As a very simple example, let H be the collection of nonempty subsets of {0, 1}, i.e., H = { {0}, {1}, {0,1} }. Then H has the two distinct choice functions f1 and f2 given by:

f1({0}) = 0
f1({1}) = 1
f1({0, 1}) = 0

f2({0}) = 0
f2({1}) = 1
f2({0, 1}) = 1

A more interesting example of a choice function is provided by taking H to be the set of (unordered) pairs of real numbers and the function to be that assigning to each pair its least element. A different choice function is obtained by assigning to each pair its greatest element. Clearly many more choice functions on H can be defined.

Stated in terms of choice functions, Zermelo's first formulation of AC reads:

AC1:
Any collection of nonempty sets has a choice function.

AC1 can be reformulated in terms of indexed or variable sets. An indexed collection of sets A = {Ai : i ∈ I} may be conceived as a variable set, to wit, as a set varying over the index set I. Each Ai is then the “value” of the variable set A at stage i. A choice function on A is a map f : I → ∪i∈I Ai such that f(i) ∈ Ai for all i ∈ I. A choice function on A is thus a “choice” of an element of the variable set A at each stage; in other words, a choice function on A is a variable element of A. AC1 is then equivalent to the assertion

AC2:
Any indexed collection of sets has a choice function.

Informally speaking, AC2 amounts to the assertion that a variable set with an element at each stage has a variable element.

AC1 can also be reformulated in terms of relations, viz.

AC3:
For any relation R between sets A, B,
    ∀x∈A∃y∈B[R(x,y)] ⇒ ∃f[f : A → B  &  ∀x∈A[R(x, fx)] ].

In other words, every relation contains a function having the same domain.

Finally AC3 is easily shown to be equivalent (in the usual set theories) to:[2]

AC4:
Any surjective function has a right inverse.
In a 1908 paper Zermelo introduced a modified form of AC. Let us call a transversal (or choice set) for a family of sets H any subset T ⊆ ∪H for which each intersection T ∩ X for X ∈ H has exactly one element. As a very simple example, let H = {{0}, {1}, {2, 3}}. Then H has the two transversals {0, 1, 2} and {0, 1, 3}. A more substantial example is afforded by letting H be the collection of all lines in the Euclidean plane parallel to the x-axis. Then the set T of points on the y-axis is a transversal for H.

Stated in terms of transversals, then, Zermelo's second (1908) formulation of AC amounts to the assertion that any family of mutually disjoint nonempty sets has a transversal.[3]

Zermelo asserts that “the purely objective character” of this principle “is immediately evident.” In making this assertion Zermelo meant to emphasize the fact that in this form the principle makes no appeal to the possibility of making "choices". It may also be that Zermelo had the following “combinatorial” justification of the principle in mind. Given a family H of mutually disjoint nonempty sets, call a subset S ⊆ ∪H a selector for H if S ∩ X ≠ Ø for all X ∈ H. Clearly selectors for H exist; ∪H itself is an example. Now one can imagine taking a selector S for H and “thinning out” each intersection S ∩ X for X ∈ H until it contains just a single element. The result is a transversal for H. This argument, suitably refined, yields a precise derivation of AC in this formulation from the set-theoretical principle known as Zorn's lemma (see below).

Let us call Zermelo's 1908 formulation the combinatorial axiom of choice:

CAC:
Any collection of mutually disjoint nonempty sets has a transversal.

It is to be noted that AC1 and CAC for finite collections of sets are both provable (by induction) in the usual set theories. But in the case of an infinite collection, even when each of its members is finite, the question of the existence of a choice function or a transversal is problematic[4]. For example, as already mentioned, it is easy to come up with a choice function for the collection of pairs of real numbers (simply choose the smaller element of each pair). But it is by no means obvious how to produce a choice function for the collection of pairs of arbitrary sets of real numbers.

Zermelo's original purpose in introducing AC was to establish a central principle of Cantor's set theory, namely, that every set admits a well-ordering and so can also be assigned a cardinal number. Zermelo's 1904 introduction of the axiom, as well as the use to which he put it, provoked considerable criticism from the mathematicians of the day. The chief objection raised was to what some saw as its highly non-constructive, even idealist, character: while the axiom asserts the possibility of making a number of — perhaps even an uncountable number — of arbitrary “choices”, it gives no indication whatsoever of how these latter are actually to be effected, of how, otherwise put, choice functions are to be defined. This was particularly objectionable to mathematicians of a “constructive” bent such as the so-called French Empiricists Baire, Borel and Lebesgue, for whom a mathematical object could be asserted to exist only if it can be defined in such a way as to characterize it uniquely. Zermelo's response to his critics came in the form in two papers in 1908. In the first of these, as remarked above, he reformulated in which he reformulated AC in terms of transversals; in the second (1908a) he made explicit the further assumptions needed to carry through his proof of the well-ordering theorem. These assumptions constituted the first explicit presentation of an axiom system for set theory.

As the debate concerning the Axiom of Choice rumbled on, it became apparent that the proofs of a number of significant mathetical theorems made essential use of it, thereby leading many mathematicians to treat it as an indispensable tool of their trade. Hilbert, for example, came to regard AC as an essential principle of mathematics[5] and employed it in his defence of classical mathematical reasoning against the attacks of the intuitionists. Indeed his ε-operators are essentially just choice functions (see the entry on the epsilon calculus).

Although the usefulness of AC quickly become clear, doubts about its soundness remained. These doubts were reinforced by the fact that it had certain strikingly counterintuitive consequences. The most spectacular of these was Banach and Tarski's paradoxical decompositions of the sphere (Banach and Tarski 1924): any solid sphere can be split into finitely many pieces which can be reassembled to form two solid spheres of the same size; and any solid sphere can be split into finitely many pieces in such a way as to enable them to be reassembled to form a solid sphere of arbitrary size. (See Wagon 1993.)

It was not until the middle 1930s that the question of the soundness of AC was finally put to rest with Kurt Gödel's proof of its consistency relative to the other axioms of set theory.

Here is a brief chronology of AC:[6]

1904/1908 Zermelo introduces axioms of set theory, explicitly formulates AC and uses it to prove the well-ordering theorem, thereby raising a storm of controversy.
1904 Russell recognizes AC as the multiplicative axiom: the product of arbitrary nonzero cardinal numbers is nonzero.
1914 Hausdorff derives from AC the existence of nonmeasurable sets in the “paradoxical” form that ½ of a sphere is congruent to 1/3 of it (Hausdorff 1914).
1922 Fraenkel introduces the “permutation method” to establish independence of AC from a system of set theory with atoms (Fraenkel 1922).
1924 Building on the work of Hausdorff, Banach and Tarski derive from AC their paradoxical decompositions of the sphere.
1926 Hilbert introduces into his proof theory the “transfinite” or “epsilon” axiom as a version of AC . (Hilbert 1926).
1936 Lindenbaum and Mostowski extend and refine Fraenkel's permutation method, and prove the independence of various statements of set theory weaker than AC . (Lindenbaum and Tarski 1938)
1935–38 Gödel establishes relative consistency of AC with the axioms of set theory (Gödel 1938, 1939, 1940).
1950s Mendelson, Shoenfield and Specker, working independently, use the permutation method to establish the independence of various forms of AC from a system of set theory without atoms, but also lacking the axiom of foundation (Mendelson 1956, 1958, Shoenfield 1955, Specker 1957).
1963 Paul Cohen proves independence of AC from the standard axioms of set theory (Cohen 1963, 1963a, 1964).

2. Independence and Consistency of the Axiom of Choice

As stated above, in 1922 Fraenkel proved the independence of AC from a system of set theory containing “atoms”. Here by an atom is meant a pure individual, that is, an entity having no members and yet distinct from the empty set (so a fortiori an atom cannot be a set). In a system of set theory with atoms it is assumed that one is given an infinite set A of atoms. One can build a universe V(A) of sets over A by starting with A, adding all the subsets of A, adjoining all the subsets of the result, etc., and iterating transfinitely. V(A) is then a model of set theory with atoms. The kernel of Fraenkel's method for proving the independence of AC is the observation that, since atoms cannot be set-theoretically distinguished, any permutation of the set A of atoms induces a structure-preserving permutation — an automorphism — of the universe V(A) of sets built from A. This idea may be used to construct another model Sym(V) of set theory — a permutation or symmetric model — in which a set of mutually disjoint pairs of elements of A has no choice function.

Now let us suppose that we are given a group G of automorphisms of A. Let us say that an automorphism π of A fixes an element x of V(A) if π(x) = x. Clearly, if π ∈ G fixes every element of A, it also fixes every element of V(A). Now it may be the case that, for certain elements x ∈ V(A), the fixing of the elements of a subset of A by any π ∈ G suffices to fix x. We are therefore led to define a support for x to be a subset X of A such that, whenever π ∈ G fixes each member of X, it also fixes x. Members of V(A) possessing a finite support are called symmetric.

We next define the universe Sym(V) to consist of the hereditarily symmetric members of V(A), that is, those x ∈ V(A) such that x, the elements of x, the elements of elements of x, etc., are all symmetric. Sym(V) is also a model of set theory with set of atoms A, and π induces an automorphism of Sym(V).

Now suppose A to be partitioned into a (necessarily infinite) mutually disjoint set P of pairs. Take G to be the group of permutations of A which fix all the pairs in P. Then P ∈ Sym(V); it can now be shown that Sym(V) contains no choice function on P. For suppose f were a choice function on P and f ∈ Sym(V). Then f has a finite support which may be taken to be of the form {a1, …, an, b1,…,bn} with each pair {ai, bi} ∈ P. Since P is infinite, we may select a pair {c, d} = U from P different from all the {ai, bi}. Now we define π ∈ G so that π fixes each ai and bi and interchanges c and d. Then π also fixes f. Since f was supposed to be a choice function on P, and U ∈ P, we must have f(U) ∈ U, that is, f(U) = c or f(U) = d. Since π interchanges c and d, it follows that π(f(U)) ≠ f(U). But since π is an automorphism, it also preserves function application, so that π(f(U)) = πf (π(U)). But π(U) = U and πf = f, whence π(f(U)) = f(U). We have duly arrived at a contradiction, showing that the universe Sym(V) contains no choice function on P.

The point here is that for a symmetric function f defined on P there is a finite list L of pairs from P the fixing of all of whose elements suffices to fix f, and hence also all the values of f. Now, for any pair U in P but not in L , a permutation π can always be found which fixes all the elements of the pairs in L, but does not fix the members of U. Since π must fix the value of f at U, that value cannot lie in U. Therefore f cannot “choose” an element of U, so a fortiori f cannot be a choice function on P.

This argument shows that collections of sets of atoms need not necessarily have choice functions, but it fails to establish the same fact for the “usual” sets of mathematics, for example the set of real numbers. This had to wait until 1963 when Paul Cohen showed that it is consistent with the standard axioms of set theory (which preclude the existence of atoms) to assume that a countable collection of pairs of sets of real numbers fails to have a choice function. The core of Cohen's method of proof — the celebrated method of forcing — was vastly more general than any previous technique; nevertheless his independence proof also made essential use of permutation and symmetry in essentially the form in which Fraenkel had originally employed them.

Gödel's proof of the relative consistency of AC with the axioms of set theory (see the entry on Kurt Gödel) rests on an entirely different idea: that of definability. He introduced a new hierarchy of sets — the constructible hierarchy — by analogy with the cumulative type hierarchy. We recall that the latter is defined by the following recursion on the ordinals, where P(X) is the power set of X, α is an ordinal, and λ is a limit ordinal::

V0 = Ø
Vα+1 = P(Vα)
Vλ = ∪α<λ Vα

The constructible hierarchy is defined by a similar recursion on the ordinals, where Def(X) is the set of all subsets of X which are first-order definable in the structure (X, ∈, (x)x∈X):[7]

L0 = Ø
Lα+1 = Def(Lα)
Lλ = ∪α<λ Lα

The constructible universe is the class L = ∪α∈Ord Lα; the members of L are the constructible sets. Gödel showed that (assuming the axioms of Zermelo-Fraenkel set theory ZF) the structure (L, ∈) is a model of ZF and also of AC as well as the Generalized Continuum Hypothesis). The relative consistency of AC with ZF follows.

It was also observed by Gödel (1964) (and, independently, by Myhill and Scott 1971, Takeuti 1963 and Post 1951) that a simpler proof of the relative consistency of AC can be formulated in terms of ordinal definability. If we write D(X) for the set of all subsets of X which are first-order definable in the structure (X, ∈), then the class OD of ordinal definable sets is defined to be the union ∪α∈Ord D(Vα). The class HOD of hereditarily ordinal definable sets consists of all sets a for which a, the members of a, the members of members of a, … etc., are all ordinal definable. It can then be shown that the structure (HOD, ∈) is a model of ZF + AC , from which the relative consistency of AC with ZF again follows.[8]

3. Maximal Principles and Zorn's Lemma

The Axiom of Choice is closely allied to a group of mathematical propositions collectively known as maximal principles. Broadly speaking, these propositions assert that certain conditions are sufficient to ensure that a partially ordered set contains at least one maximal element, that is, an element such that, with respect to the given partial ordering, no element strictly exceeds it.

To see the connection between the idea of a maximal element and AC, let us return to the latter's formulation AC2 in terms of indexed sets. Accordingly suppose we are given an indexed family of nonempty sets A = {Ai : i ∈ I}. Let us define a potential choice function on A to be a function f whose domain is a subset of I such that f(i) ∈ Ai for all i ∈ J. (Here the use of the qualifier potential is suggested by the fact that the domain is a subset of I; recall that a choice function f on A has the same properties as what we are now calling potential choice functions except that the domain of f is required to be all of I, not just a subset.) The set P of potential choice functions on A can be partially ordered by inclusion: we agree that, for potential choice functions f, g ∈ P, the relation f ≤ g holds provided that the domain of f is included in that of g and the value of f at an element of its domain coincides with the value of g there. It is now easy to see that the maximal elements of P with respect to the partial ordering ≤ are precisely the choice functions on A.

Zorn's Lemma is the best-known principle ensuring the existence of such maximal elements. To state it, we need a few definitions. Given a partially ordered set (P, ≤), an upper bound for a subset X of P is an element a ∈ P for which x ≤ a for every x ∈ X; a maximal element of P may then be defined as an element a for which the set of upper bounds of {a} coincides with {a}, which essentially means that no element of P is strictly larger than a. A chain in (P,≤) is a subset C of P such that, for any x, y ∈ P, either x ≤ y or y ≤ x. P is said to be inductive if every chain in P has an upper bound. Now Zorn's Lemma asserts:

Zorn's Lemma (ZL):
Every nonempty inductive partially ordered set has a maximal element.

Why is Zorn's Lemma plausible? Here is an informal argument. Given a nonempty inductive partially ordered set (P, ≤), pick an arbitrary element p0 of P. If p0 is maximal, stop there. Otherwise pick an element p1 > p0; if p1 is maximal, stop there. Otherwise pick an element p2 > p1, and repeat the process. If none of the elements p0 < p1 < p2 < … < pn < … is maximal, the pi form a chain which, since P is inductive, has an upper bound q0. If q0 is maximal, stop there. Otherwise the procedure can be repeated with q0 < q1,…, and then iterated. This process must eventually terminate, since otherwise the union of the chains so generated would constitute a proper class, making P itself a proper class contrary to assumption. The point at which the process terminates yields a maximal element of P.

This argument, suitably rigorized, gives a proof[9] of ZL from AC1 in Zermelo-Fraenkel set theory: in this proof AC1 is used to “pick” the elements referred to in the informal argument.

Another version of Zorn's Lemma can be given in terms of collections of sets. Given a collection H of sets, let us call a nest in H any subcollection N of H such that, for any pair of members of N, one is included in the other.[10] Call H strongly inductive if the union of any nest in H is a member of H. Zorn's Lemma may then be equivalently restated as the assertion that any nonempty strongly inductive collection H of sets has a maximal member, that is, a member properly included in no member of H. This may in turn be formulated in a dual form. Call a family of sets strongly reductive if it is closed under intersections of nests. Then any nonempty strongly reductive family of sets has a minimal element, that is, a member properly including no member of the family.

AC2 is now easily derived from Zorn's Lemma in this alternative form. For the set P of potential choice functions on an indexed family of sets A is clearly nonempty and is readily shown to be strongly inductive; so Zorn's lemma yields the existence of a choice function on A.

CAC can be derived from ZL in a way echoing the “combinatorial” justification of CAC sketched above. Accordingly suppose we are given a family H of mutually disjoint nonempty sets; call a subset S ⊆ ∪H a sampling for H if, for any X ∈ H, either X ⊆ S or S ∩ X is nonempty and finite. Minimal samplings are precisely transversals for H;[11] and the collection T of samplings is clearly nonempty since it contains ∪H. So if it can be shown that T is strongly reductive,[12] Zorn's lemma will yield a minimal element of T and so a transversal for H. The strong reductiveness of T may be seen as follows: suppose that {Si : i ∈ I} is a nest of samplings; let S = ∩i∈ISi. We need to show that S is itself a sampling; to this end let X ∈ H and suppose ¬(X ⊆ S). Then there is i ∈ I for which ¬(X ⊆ Si); since Si is a sampling, Si ∩ X is finite (JAA: suggested addition: "and") nonempty, say Si ∩ X = {x1, …, xn}. Clearly S ∩ X is then finite; suppose for the sake of contradiction that S ∩ X = Ø. Then for each k = 1, …, n there is ik ∈ I for which ¬(xk ∈ Sik). It follows that ¬(Si ⊆ Sik), for k = 1, …, n. So, since the Si form a chain, each Sik is a subset of Si. Let Sj be the least of Si1, … , Sik; then Sj ⊆ Si. But since ¬(xk ∈ Sj), for k = 1, …, n, it now follows that Sj ∩ X = Ø, contradicting the fact that Sj is a sampling. Therefore S ∩ X ≠ Ø; and S is a sampling as claimed.

We note that while Zorn's lemma and the Axiom of Choice are set-theoretically equivalent, it is much more difficult to derive the former from the latter than vice-versa.

Here is a brief chronology of maximal principles.

1909 Hausdorff introduces first explicit formulation of a maximal principle and derives it from AC (Hausdorff 1909)(
1914 Hausdorff's Grundzüge der Mengenlehre (one of the first books on set theory and general topology) includes several maximal principles.
1922 Kuratowski formulates and employs several maximal principles in avoiding use of transfinite ordinals (Kuratowski 1922).
1926–28 Bochner and others independently introduce maximal principles (Bochner 1928, Moore 1932).
1935 Max Zorn, apparently unacquainted with previous formulations of maximal principles, publishes (Zorn 1935) his definitive version thereof later to become celebrated as his lemma (ZL). ZL was first formulated in Hamburg in 1933, where Chevalley and Artin quickly “adopted” it. It seems to have been Artin who first recognized that ZL would yield AC, so that the two are equivalent (over the remaining axioms of set theory). Zorn regarded his principle less as a theorem than as an axiom — he hoped that it would supersede cumbersome applications in algebra of transfinite induction and well-ordering, which algebraists in the Noether school had come to regard as “transcendental” devices.
1939–40 Teichmüller, Bourbaki and Tukey independently reformulate ZL in terms of “properties of finite character”(Bourbaki 1939, Teichmuller 1939, Tukey 1940).

4. Mathematical Applications of the Axiom of Choice

The Axiom of Choice has numerous applications in mathematics, a number of which have proved to be formally equivalent to it[13]. Historically the most important application was the first, namely:

After Zermelo published his 1904 proof of the well-ordering theorem from AC, it was quickly seen that the two are equivalent.

Another early equivalent of AC is

Early applications of ACinclude:

A significant “folklore” equivalent of ACis

A much-studied special case of AC is the

Mathematical equivalents of AC include:

There are a number of mathematical consequences of AC which are known to be weaker[14] than it, in particular:

Finally, there is

The question of the equivalence of this with AC is one of the few remaining interesting open questions in this area; while it clearly implies BPI, it was proved independent of BPI in Bell 1983.

Many of these theorems are discussed in Bell and Machover (1977).

5. The Axiom of Choice and Logic

An initial connection between AC and logic emerges by returning to its formulation AC3 in terms of relations, namely: any binary relation contains a function with the same domain. This version of AC is naturally expressible within a second-order language L with individual variables x, y, z, … and function variables f, g, h, …. In L, binary relations are represented by formulas φ(x, y) with two free individual variables x, y. The counterpart in L of the assertion AC3 is then

ACL:
∀x ∃y φ(x, y) → ∃f ∀x φ(x, fx).

This scheme of sentences is the standard logical form of AC.

Zermelo's original form of the Axiom of Choice, AC1, can be expressed as a scheme of sentences within a suitably strengthened version of L. Accordingly we now suppose L to contain in addition predicate variables X, Y, Z, … and second-order function variables F, G, H, …. Here a second-order function variable F may be applied to a predicate variable X to yield an individual term FX. The scheme of sentences

AC1L:
∀X [Φ(X) → ∃x X(x)] → ∃F ∀X[Φ(X) → X(FX)]

is the direct counterpart of AC1 in this strengthened second-order language. In words, AC1L asserts that, if each predicate having a certain property Φ has instances, then there is a function F on predicates such that, for any predicate X satisfying Φ, FX is an instance of X. Here predicates are playing the role of sets.

Up to now we have tacitly assumed our background logic to be the usual classical logic. But the true depth of the connection between AC and logic emerges only when intuitionistic or constructive logic is brought into the picture. It is a remarkable fact that, assuming only the framework of intuitionistic logic together with certain mild further presuppositions, the Axiom of Choice can be shown to entail the cardinal rule of classical logic, the law of excluded middle — the assertion that A ∨ ¬A for any proposition A. To be precise, using the rules of intuitionistic logic within our augmented language L, we shall derive[16] the law of excluded middle from AC1L conjoined with the following additional principles:

Predicative Comprehension:
∃X ∀x[X(x) ↔ φ(x)] , where φ contains no bound function or predicate variables.

Extensionality of Functions:
∀X ∀Y ∀F[X ≈ Y → FX = FY], where X ≈ Y is an abbreviation for ∀x[X(x) ↔ Y(x)], that is, X and Y are extensionally equivalent.

Two Distinct Individuals:
0 ≠ 1, where 0 and 1 are individual constants.

Now let A be a given proposition. By Predicative Comprehension, we may introduce predicate constants U, V together with the assertions

(1) ∀x[U(x) ↔ (A ∨ x =0)] ∀x[V(x) ↔ (A ∨ x = 1)]

Let Φ(X) be the formula X ≈ U ∨ X ≈ V. Then clearly we may assert ∀X[Φ(X) → ∃xX(x)] so AC1L may be invoked to assert ∃F ∀X[Φ(X) → X(FX)]. Now we can introduce a function constant K together with the assertion

(2) ∀X[Φ(X) → X(KX)].

Since evidently we may assert Φ(U) and Φ(V), it follows from (2) that we may assert U(KU) and V(KV), whence also, using (1),

[A ∨ KU = 0 ] ∧ [A ∨ KV = 1].

Using the distributive law (which holds in intuitionistic logic), it follows that we may assert

A ∨ [KU = 0 ∧ KV = 1].

From the presupposition that 0 ≠ 1 it follows that

(3) A ∨ KU ≠ KV

is assertable. But it follows from (1) that we may assert A → U ≈ V, and so also, using the Extensionality of Functions, A → KU = KV. This yields the assertability of KU ≠ KV → ¬A, which, together with (3) in turn yields the assertability of

A ∨ ¬A,

that is, the law of excluded middle.

The fact that the Axiom of Choice implies Excluded Middle seems at first sight to be at variance with the fact that the former is often taken as a valid principle in systems of constructive mathematics governed by intuitionistic logic, e.g. Bishop's Constructive Analysis[17] and Martin-Löf's Constructive Type Theory[18], in which Excluded Middle is not affirmed. In Bishop's words, “A choice function exists in constructive mathematics because a choice is implied by the very meaning of existence.” Thus, for example, the antecedent ∀x ∃y φ(x, y) of ACL, given a constructive construal, just means that we have a procedure which, applied to each x, yields a y for which φ(x, y). But this is precisely what is expressed by the consequent ∃f ∀x φ(x, fx) of ACL.

To resolve the difficulty, we note that in deriving Excluded Middle from ACL1 essential use was made of the principles of Predicative Comprehension and Extensionality of Functions[19]. It follows that, in systems of constructive mathematics affirming AC (but not Excluded Middle) either the principle of Predicative Comprehension or the principle of Extensionality of Functions must fail. While the principle of Predicative Comprehension can be given a constructive justification, no such justification can be provided for the principle of Extensionality of Functions. Functions on predicates are given intensionally, and satisfy just the corresponding principle of Intensionality ∀X ∀Y ∀F[X = Y → FX = FY]. The principle of Extensionality can easily be made to fail by considering, for example, the predicates P: rational featherless biped and Q: human being and the function K on predicates which assigns to each predicate the number of words in its description. Then we can agree that P ≈ Q but KP = 3 and KQ = 2.

In intuitionistic set theory (that is, set theory based on intuitionistic as opposed to classical logic - we shall abbreviate this as IST) and in topos theory the principles of Predicative Comprehension and Extensionality of Functions (both appropriately construed) hold and so there AC implies Excluded Middle.[20] , [21]

The derivation of Excluded Middle from AC was first given by Diaconescu (1975) in a category-theoretic setting. His proof employed essentially different ideas from the proof presented above; in particular, it makes no use of extensionality principles but instead employs the idea of the quotient of an object (or set) by an equivalence relation. It is instructive to formulate Diaconescu's argument within IST. To do this, let us call a subset U of a set A detachable if there is a subset V of A for which U ∩ V = Ø and U ∪ V = A. Diaconescu's argument amounts to a derivation from AC4 (see above) of the assertion that every subset of a set is detachable, from which Excluded Middle readily follows. Here it is.

First, given U ⊆ A, an indicator for U (in A) is a map g: A × 2 → 2 satisfying

U = { x ∈ A : g(x,0) = g(x,1) }

It is then easy to show that a subset is detachable if and only if it has an indicator.

Now we show that, if AC4 holds, then any subset of a set has an indicator, and hence is detachable.

For U ⊆ A, let R be the binary relation on A + A = A × {0} ∪ A × {1} given by

R = { ((x,0),(x,0) : x ∈ A } ∪ { ((x,1),(x,1)) : x ∈ A } ∪ { ((x,0),(x,1) : x ∈ A } ∪ { ((x,1),(x,0) : x ∈ A

It can be checked that R is an equivalence relation. Write r for the natural map from A + A to the quotient[22] Q of (A + A) by R which carries each member of A + A to its R-equivalence class.

Now apply AC4 to obtain a map f: Q → A + A satisfying f(X) ∈ X for all X ∈ Q. It is then not hard to show that, writing π1 for projection on the first coordinate,

(*) for n = 0, 1 and x ∈A, π1(f(r(x, n)) = x;

and

(**) x ∈ U ↔ f(r(x,0)) = f(r(x,1)).

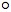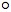Now define g: A × 2 → 2 by g = π2 compose f compose r, where π2 is projection on the second coordinate. Then g is an indicator for U, as the following equivalences show:

x ∈ U ↔ f(r(x,0)) = f(r(x,1)) … by (**)
↔ π1(f(r(x,0))) = π1(f(r(x,1))) ∧ π2(f(r(x,0))) = π2(f(r(x,1)))
↔ π2(f(r(x,0))) = π2(f(f(x,1))) … using (*)
↔ g(x,0) = g(x,1).

The proof is complete.

It can be shown (Bell 2006) that each of a number of intuitionistically invalid logical principles, including the law of excluded middle, is equivalent (in intuitionistic set theory) to a suitably weakened version of the axiom of choice. Accordingly these logical principles may be viewed as choice principles.

Here are the logical principles at issue:

SLEM α ∨ ¬ α (α any sentence)
Lin (α → β) ∨ (β → α) (α, β any sentences)
Stone ¬ α ∨ ¬¬ α (α any sentence)
Ex ∃x[ ∃x α(x) → α(x)] (α(x) any formula with at most x free)
Un ∃x[α(x) → ∀xα(x)] (α(x) any formula with at most x free)
Dis ∀x[α ∨ β(x)] → α ∨ ∀xβ(x) (α any sentence, β(x) any formula with at most x free)

Over intuitionistic logic, Lin, Stone and Ex are consequences of SLEM; and Un implies Dis. All of these schemes follow, of course, from the full law of excluded middle, that is SLEM for arbitrary formulas.

In what follows the empty set is denoted by 0, {0} by 1, and {0, 1} by 2.

We formulate the following choice principles — here X is an arbitrary set, Fun(X) the class of functions with domain X and φ(x,y) an arbitrary formula of the language of set theory with at most the free variables x, y:

ACX ∀x∈X ∃y φ(x,y) → ∃f ∈ Fun(X) ∀x ∈ X φ(x,fx)
AC*X ∃f ∈ Fun(X) [∀x ∈ X ∃y φ(x,y) → ∀x ∈ X φ(x,fx)]
DACX ∀f ∈ Fun(X) ∃x ∈ X φ(x,fx) → ∃x ∈ X ∀y φ(x,y)
DAC*X ∃f ∈ Fun(X) [∃x ∈ X φ(x,fx) → ∃x ∈ X ∀y φ(x,y)]

The first two of these are forms of AC for X; while classically equivalent, in IST AC*X implies ACX, but not conversely. The principles DACX and DAC*X are dual forms of the axiom of choice for X: classically they are both equivalent to ACX and AC*X but intuitionistically DAC*X implies DACX, and not conversely.

We also formulate the weak extensional selection principle, in which α(x) and β(x) are any formulas with at most the variable x free:

WESP:
∃x ∈ 2 α(x) ∧ ∃x ∈ 2 β(x) → ∃x ∈ 2 ∃y ∈ 2 [α(x) ∧ β(y) ∧ [∀x ∈ 2 [α(x) ↔ β(x)] → x = y]].

This principle, a straightforward consequence of the axiom of choice, asserts that, for any pair of instantiated properties of members of 2, instances may be assigned to the properties in a manner that depends just on their extensions.

Each of the logical principles tabulated above is equivalent (in IST) to a choice principle. In fact:

Further, while DAC1 is easily seen to be provable in IST, we have

Next, while AC2 is easily proved in IST, by contrast we have

In order to provide choice schemes equivalent to Lin and Stone we introduce

ac*X:
∃f ∈ 2X [∀x ∈ X ∃y ∈ 2 φ(x,y) → ∃x ∈ X φ(x,fx)]

wac*X:
∃f ∈ 2X [∀x ∈ X ∃y ∈ 2 φ(x,y) → ∀x ∈ X φ(x,fx)] provided it is provable in IST that ∀x[φ(x,0) → ¬φ(x,1)]

Clearly ac*X is equivalent to

∃f ∈ 2X[∀x ∈ X[φ(x,0) ∨ φ(x,1)] → ∀x ∈ X φ(x,fx)]

and similarly for dac*X.

Then, over IST, ac*1 and dac*1 are equivalent, respectively, to Lin and Stone.

These results show just how deeply choice principles interact with logic, when the background logic is assumed to be intuitionistic. In a classical setting where the Law of Excluded Middle is assumed these connections are obliterated.

Readers interested in the topic of the axiom of choice and type theory may consult the following supplementary document:

The Axiom of Choice and Type Theory

Bibliography

Other Internet Resources

Related Entries

category theory | Gödel, Kurt | logic, history of: intuitionistic logic | logic: intuitionistic | mathematics: constructive | set theory: constructive and Intuitionistic ZF | set theory: development of axiomatic | type theory: constructive

Acknowledgments

The author and editors would like to thank Jesse Alama for carefully reading this piece and making many valuable suggestions for improvement.