Stanford Encyclopedia of Philosophy
This is a file in the archives of the Stanford Encyclopedia of Philosophy.

Paraconsistent Logic

First published Tue Sep 24, 1996; substantive revision Wed Nov 21, 2007

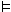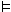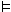The development of paraconsistent logic was initiated in order to challenge the logical principle that anything follows from contradictory premises, ex contradictione quodlibet (ECQ). Let models be a relation of logical consequence, defined either semantically or proof-theoretically. Let us say that models is explosive iff for every formula A and B, {A , ~A} models B. Classical logic, intuitionistic logic, and most other standard logics are explosive. A logic is said to be paraconsistent iff its relation of logical consequence is not explosive.

The modern history of paraconsistent logic is relatively short. Yet the subject has already been shown to be an important development in logic for many reasons. These involve the motivations for the subject, its philosophical implications and its applications. In the first half of this article, we will review some of these. In the second, we will give some idea of the basic technical constructions involved in paraconsistent logics. Further discussion can be found in the references given at the end of the article.

Motivation and Applications

Inconsistent but Non-Trivial Theories

A most telling reason for paraconsistent logic is the fact that there are theories which are inconsistent but non-trivial. Clearly, once we admit the existence of such theories, their underlying logics must be paraconsistent. Examples of inconsistent but non-trivial theories are easy to produce. An example can be derived from the history of science. (In fact, many examples can be given from this area.) Consider Bohr's theory of the atom. According to this, an electron orbits the nucleus of the atom without radiating energy. However, according to Maxwell's equations, which formed an integral part of the theory, an electron which is accelerating in orbit must radiate energy. Hence Bohr's account of the behaviour of the atom was inconsistent. Yet, patently, not everything concerning the behavior of electrons was inferred from it. Hence, whatever inference mechanism it was that underlay it, this must have been paraconsistent.

Dialetheias (True Contradictions)

The importance of paraconsistent logic also follows if, more contentiously, but as some people have argued, there are true contradictions (dialetheias), i.e., there are sentences, A, such that both A and ~A are true. If there are dialetheias then some inferences of the form {A , ~A}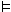 models B must fail. For only true conclusions follow validly from the true premises. Hence logic has to be paraconsistent. A plausible example of dialetheia is the liar paradox. Consider the sentence: This sentence is not true. There are two options: either the sentence is true or it is not. Suppose it is true. Then what it says is the case. Hence the sentence is not true. Suppose, on the other hand, it is not true. This is what it says. Hence the sentence is true. In either case it is both true and not true. See the entry on dialetheism in this encyclopedia for further details.

Automated Reasoning

Paraconsistent logic is motivated not only by philosophical considerations, but also by its applications and implications. One of the applications is automated reasoning (information processing). Consider a computer which stores a large amount of information. While the computer stores the information, it is also used to operate on it, and, crucially, to infer from it. Now it is quite common for the computer to contain inconsistent information, because of mistakes by the data entry operators or because of multiple sourcing. This is certainly a problem for database operations with theorem-provers, and so has drawn much attention from computer scientists. Techniques for removing inconsistent information have been investigated. Yet all have limited applicability, and, in any case, are not guaranteed to produce consistency. (There is no algorithm for logical falsehood.) Hence, even if steps are taken to get rid of contradictions when they are found, an underlying paraconsistent logic is desirable if hidden contradictions are not to generate spurious answers to queries.

Belief Revision

As a part of artificial intelligence research, belief revision is one of the areas that have been studied widely. Belief revision is the study of rationally revising bodies of belief in the light of new evidence. Notoriously, people have inconsistent beliefs. They may even be rational in doing so. For example, there may be apparently overwhelming evidence for both something and its negation. There may even be cases where it is in principle impossible to eliminate such inconsistency. For example, consider the "paradox of the preface". A rational person, after thorough research, writes a book in which they claim A1,…, An. But they are also aware that no book of any complexity contains only truths. So they rationally believe ~(A1 &…& An) too. Hence, principles of rational belief revision must work on inconsistent sets of beliefs. Standard accounts of belief revision, e.g., that of Gärdenfors et al., all fail to do this since they are based on classical logic. A more adequate account is based on a paraconsistent logic.

Mathematical Significance

Other applications of paraconsistent logic concern theories of mathematical significance. Examples of such theories are formal semantics and set theory.

Semantics is the study that aims to spell out a theoretical understanding of meaning. Most accounts of semantics insist that to spell out the meaning of a sentence is, in some sense, to spell out its truth-conditions. Now, prima facie at least, truth is a predicate characterised by the Tarski T-scheme:

T(A) ↔ A,
where A is a sentence and A is its name. But given any standard means of self-reference, e.g., arithmetisation, one can construct a sentence, B, which means that ~T(B). The T-scheme gives that T(B) ↔ ~T(B). It then follows that T(B) & ~T(B). (This is, of course, just the liar paradox.)

The situation is similar in set theory. The naive, and intuitively correct, axioms of set theory are the Comprehension Schema and Extensionality Principle:

∃y∀x(x ∈ y ↔ A)

∀x(x ∈ y ↔ x ∈ z) → y = z

where x does not occur free in A. As was discovered by Russell, any theory that contains the Comprehension Schema is inconsistent. For putting ‘y 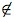not-element y’ for A in the Comprehension Schema and instantiating the existential quantifier to an arbitrary such object ‘r’ gives:
∀y(y ∈ r ↔ y not-element y)
So, instantiating the universal quantifier to ‘r’ gives:
r ∈ r ↔ r not-element r
It then follows that r ∈ r & r 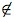not-element r.

The standard approaches to these problems of inconsistency are, by and large, ones of expedience. However, a paraconsistent approach makes it possible to have theories of truth and sethood in which the fundamental intuitions about these notions are respected. The contradictions may be allowed to arise, but these need not infect the rest of the theory.

In fact, it has recently been shown that there is a paraconsistent set theory that maintains the familiar theorems of classical mathematics (via different proofs) while admitting some contradictions. This result shows not only that paraconsistent logic can serve as an underlying logic for mathematics but also that the standard mathematics can be non-trivially inconsistent.

The Philosophical Significance of Gödel's Theorem

Paraconsistent logic also has important philosophical ramifications. One example of this concerns Gödel's theorem. One version of Gödel's first incompleteness theorem states that for any consistent axiomatic theory of arithmetic, which can be recognised to be sound, there will be an arithmetic truth - viz., its Gödel sentence - not provable in it, but which can be established as true by intuitively correct reasoning. The heart of Gödel's theorem is, in fact, a paradox that concerns the sentence, G, ‘This sentence is not provable’. If G is provable, then it is true and so not provable. Thus G is proved. Hence G is true and so unprovable. If an underlying paraconsistent logic is used to formalise the arithmetic, and the theory therefore allowed to be inconsistent, the Gödel sentence may well be provable in the theory (essentially by the above reasoning). So a paraconsistent approach to arithmetic overcomes the limitations of arithmetic that are supposed (by many) to follow from Gödel's theorem.

Systems of Paraconsistent Logic

The foregoing discussion indicates some of the motivations for paraconsistent logic, its applications and implications. We will now indicate some of the main approaches to paraconsistency. There are many different paraconsistent logics. Most of them can be defined in terms of a semantics which allows both A and ~A to hold in an interpretation. Validity is then defined in terms of the preservation of holding in an interpretation, and so ECQ fails. We will illustrate this with four kinds of propositional paraconsistent logics: non-adjunctive, non-truth-functional, many-valued, and relevant. 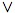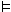(Paraconsistent quantified logics are straightforward extensions of these.) In all the following systems, not only ECQ fails, but so does the Disjunctive Syllogism (DS), defined as the following inference rule: {A, ~A vel B} models B. 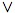In particular, then, if one defines the material conditional, A ⊃ B, as ~A vel B (as usual) then modus ponens for this fails.

Non-Adjunctive Systems

Let us start with non-adjunctive systems, so called because the inference from A and B to A & B fails. The first of these to be produced was also the first formal paraconsistent logic. This was Jaskowski's discussive (or discursive) logic. In a discourse, each participant puts forward some information, beliefs, or opinions. What is true in a discourse is the sum of opinions given by participants. Each participant's opinions are taken to be self-consistent, but may be inconsistent with those of others. To formalise this idea, take an interpretation, I, to be one for a standard modal logic, say S5. Each participant's belief set is the set of sentences true in a possible world in I. Thus, A holds in I iff A holds at some world in I. Clearly, one may have both A and ~A (but not A & ~A) holding in an interpretation. Since modus ponens for ⊃ fails, Jaskowski introduced a connective he called discussive implication, ⊃d, defined as (DiamondA ⊃ B). It is easy to check that in S5 discussive implication satisfies modus ponens.

Non-Truth-Functional Logics

The study of non-truth-functional systems was initiated by da Costa (who has also produced several other kinds of system). The main idea here was to maintain the apparatus of some positive logic, say classical or intuitionistic, but to allow negation in an interpretation to behave non-truth-functionally. Thus, take an interpretation to be a function which maps formulas to 1 or 0; &, 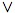vel, and → behave in the usual (classical) way, but the value of ~A is independent of that of A. In particular, both may take the value 1. Negation has no significant properties under these semantics. Various properties of negation may be obtained by adding further constraints on interpretations. If we add the requirements that, for any A, either A or ~A must take the value 1 (giving the Law of Excluded Middle) and that whenever ~~A takes the value 1, so does A, we obtain the core of da Costa's systems Ci , for finite i. If we start with an appropriate semantics for positive intuitionist logic, and proceed in the same way, we obtain da Costa's logic Cω. If we write A° for ~(A & ~A) then it is natural to take it as expressing the consistency of A. Further postulates constraining how A° behaves differentiate between the Ci systems for finite i.

Many-Valued Systems

Perhaps the simplest way of generating a paraconsistent logic, first proposed by Asenjo, is to use a many-valued logic, that is, a logic with more than two truth values. The formulas which hold in a many-valued interpretations are those which have a value said to be designated. A many-valued logic will therefore be paraconsistent if it allows both a formula and its negation to be designated. The simplest strategy is to use three truth values: true (only) and false (only), which function as in classical logic, and both truth and false (which, naturally, is a fixed point for negation). Both varieties of truth are designated. This is the approach of the paraconsistent logic LP. If one adds a fourth value, neither true nor false, which behaves in an appropriate way, one obtains Dunn's semantics for First Degree Entailment, which is a fragment of relevant logics. If one takes the truth values to be the real numbers between 0 and 1, with a suitable set of designated values, the logic will be a natural paraconsistent fuzzy logic.

Relevant Logics

Relevant logics were pioneered by Anderson and Belnap. World-semantics for them were developed by R. and V.Routley and Meyer. In an Routleys-Meyer interpretation for such logics, conjunction and disjunction behave in the usual way. But each world, w, has an associate world, w*; and ~A is true at w iff A is false, not at w, but w*. Thus, if A is true at w, but false at w*, A & ~A is true at w. To obtain the standard relevant logics, one needs to add the constraint that w** = w. As is clear, negation in these semantics is an intensional operator.

The concern with relevant logics is not so much with negation as with a conditional connective, → (satisfying modus ponens). Semantics for this are obtained by furnishing each interpretation with a ternary relation, R. In the simplified semantics of Priest, Sylvan and Restall, worlds are divided into normal and non-normal. If w is a normal world, A → B is true at w iff at all worlds where A is true, B is true. If w is non-normal, A → B is true at w iff for all x, y, such that Rwxy, if A is true at x, B is true at y. (Validity is defined as truth preservation over normal worlds.) This gives the basic relevant logic, B. Stronger logics, such as the logic R, are obtained by adding constraints on the ternary relation.

There are also versions of world-semantics for relevant logics based on Dunn's four-valued semantics for First Degree Entailment. In these, an evaluation is a relation between a formula and {true, false} rather than a function. Then negation is extensional. For a conditional connective, it seems natural to define it as: A → B is true at w iff for all x, y, such that Rwxy, if A is true at x, B is true at y; and A → B is false at w iff for some x, y, such that Rwxy, if A is true at x, B is false at y. Adding various constraints on the ternary relation provides stronger logics. However, these logics are not the standard relevant logics developed by Anderson and Belnap. To obtain the standard family of relevant logics, one needs neighbourhood frames. Further details concerning relevant logics can be found in the article on that topic in this encyclopedia.

Bibliography

For Paraconsistent Logic and Paraconsistency in general:

On Dialetheism

For Automated Reasoning

For Belief Revision

For Mathematical Significance and Gödel's Theorem

For Non-Adjunctive Systems

For Non-Truth-Functional Systems

For Many-Valued Systems

For Relevant Systems

Other Internet Resources

[Please contact the authors with suggestions.]

Related Entries

dialetheism [dialethism] | logic: many-valued | logic: relevance | logic: substructural | mathematics: inconsistent | Sorites paradox