Supplement to Deontic Logic
SDL Containment Proof
Recall SDL:
A1: All tautologous wffs of the language (TAUT) A2: OB(p → q) → (OBp → OBq) (OB-K) A3: OBp → ~OB~p (OB-NC) R1: If p and
p → q then
q
(MP) R2: If p then
OBp
(OB-NEC)
We have already shown OB-NC is derivable in
Kd above, and TAUT and MP are given, since they hold for
all formulas of Kd. So we need only derive
OB-K and OB-NEC of SDL, which we
will do in reverse order. Note that RM,
if 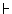 r → s,
then
r → s,
then 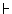 □r → □s), is derivable in
Kd, and so we rely on it in the second
proof.[1]
□r → □s), is derivable in
Kd, and so we rely on it in the second
proof.[1]
Show: Ifp then
OBp. (OB-NEC)
Proof: Assumep. It follows by PC that
d → p. So by NEC for □, we get
□(d → p), that is, OBp.
Show:OB(p → q) → (OBp → OBq). (K of SDL)
Proof: Assume OB(p → q) and OBp. From PC alone,(d → (p → q)) → [(d → p) → (d → q)]. So by RM for □, we have
□(d → (p → q)) → □[(d → p) → (d → q)]. But the antecedent of this is just, OB(p → q) in disguise, which is our first assumption. So we have □[(d → p) → (d → q)] by MP. Applying K for □ to this, we get □(d → p) → □(d → q). But the antecedent to this is just our second assumption, OBp. So by MP, we get □(d → q), that is, OBq.
Metatheorem: SDL is derivable in Kd.
Note that showing that the pure deontic fragment of Kd contains no more than SDL is a more complex matter. The proof relies on already having semantic metatheorems available. An excellent source for this is Åqvist 2002 [1984].[2]
Return to Deontic Logic.

